Navegando por mundos pequenos
Quando comecei a estudar sobre banco de dados vetorial, fiquei surpreso ao descobrir que não existe garantia de resultado ótimo. Por exemplo, ao buscar pelos \(k\) vetores mais próximos de um vetor \(v\), não é garantido que os vetores retornados serão os mais próximos do conjunto.
Seguindo meus próprios princípios, procurei saber os conceitos por trás dessas soluções e descobri sobre o HNSW (Hierarchical Navigable Small World). É um algoritmo muito interessante – que junta os conceitos de skip-list e uma estrutura de grafos – para oferecer complexidade \(log (N)\) na busca de embeddings.
Como esse algoritmo funciona e por que ele nem sempre retorna o resultado ótimo?
O problema
Uma das aplicações mais comuns para o uso de embeddings são soluções baseadas em RAG, no qual a etapa de retrieval é uma busca vetorial para alimentar a geração de resposta. É importante notar que a “busca vetorial” é, na verdade, um problema de ranqueamento: a proposta é ordernar o conteúdo por relevência e não filtrar o conjunto de dados por alguma chave de busca.
É um problema trivial para poucos vetores – basta calcular o produto interno entre o vetor da consulta e os vetores do conjunto de dados – mas não escala bem. Esse cálculo demanda uma matriz contendo todos os embeddings do conjunto de dados em memória, o que torna essa solução inviável para grandes conjuntos de dados.
A proposta do HNSW é análoga a um índice de banco de dados, criar uma estrutura de dados adicional para otimizar a recuperação de informação. A estrutura é uma hierarquia de grafos, em que cada nó representa um documento no conjunto de dados e as arestas são geradas por heurísticas com base na proximidade dos vetores.
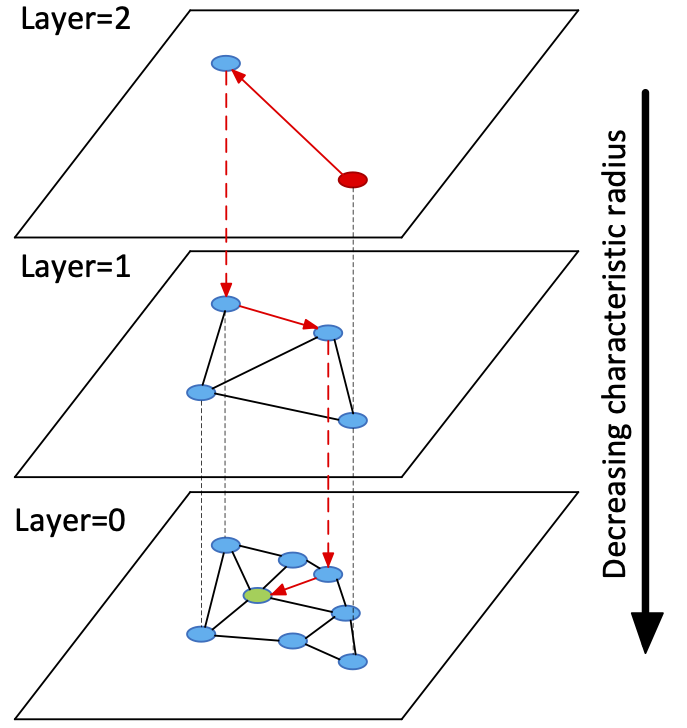
Diferente de outras estruturas de índice, ela não garante o resultado ótimo: a depender dos parâmetros de busca e criação, é possível obter respostas diferentes para uma mesma consulta e mesmo conjunto de vetores. A construção do grafo também tem processos estocásticos, construir um HNSW com os mesmos dados e parâmetros, não garante uma mesma estrutura final.
O HNSW é uma estrutura de dados com aspectos de modelo de machine learning: a performance precisa ser avaliada tanto da perspectiva de computação como pelo prisma de qualidade resultados. Erros de configuração não atrapalham apenas o tempo de resposta, mas a qualidade dela também.
Criando os pequenos mundos
Os “mundos pequenos” do HNSW são as camadas da hierarquia de grafos da estrutura. Ao inserir um ítem, a hierarquia do grafo é escolhida de forma estocástica, usando a seguinde função:
\[ \lfloor -ln(U(0,1)) \cdot m_{l} \rfloor \]
sendo \(U(0,1)\) uma distribuição uniforme no intervalo \([0,1]\) e \(m_{l}\) um hiperparâmetro no intervalo \([0,1]\). Abaixo, a implementação em Python dessa etapa:
class HNSW:
...
def __init__(self, m_max: int, m_max0: int, ef_construction: int, m_l: float):
self.layers: list[Layer] = []
self.m_max = m_max
self.m_max0 = m_max0
self.m_l = m_l
self.ef_construction = ef_construction
self.entrypoint: str | None = None
def _get_level(self) -> int:
return int(np.floor(-np.log(np.random.uniform()) * self.m_l))
def insert(self, key: str, value: list[float]):
level = self._get_level()
...
...
A estrutura do HNSW começa com zero camadas, elas são criadas à medida em que se faz necessário. Por exemplo, se o nó foi sorteado para a camada 3 e existe apenas uma camada, as duas camadas adicionais serão criadas com esse nó:
class HNSW:
def __init__(self, m_max: int, m_max0: int, ef_construction: int, m_l: float):
self.layers: list[Layer] = []
self.m_max = m_max
self.m_max0 = m_max0
self.m_l = m_l
self.ef_construction = ef_construction
self.entrypoint: str | None = None
def _get_level(self) -> int:
return int(np.floor(-np.log(np.random.uniform()) * self.m_l))
def _create_layer(self):
self.layers.append(Layer())
def insert(self, key: str, value: list[float]):
max_level = len(self.layers) - 1
level = self._get_level()
while max_level < level:
self._create_layer()
max_level = len(self.layers) - 1
...
Caso o nó a ser incluído seja sorteado para uma camada inferior, é necessário iniciar da camada superior e ir descendo até encontrar um nó que esteja presente na camada sorteada:
def insert(self, key: str, value: list[float]):
...
entrypoint: str = self.entrypoint
for level in reversed(range(level, max_level)):
entrypoint, *_ = self.layers[level].search(value, 1, entrypoint)
...
Ao chegar na camada sorteada, ela deva ser atualizada e todas as que estão abaixo da mesma. O processo consiste em selecionar os vizinhos aos quais esse nó será conectado, restrito a um hiperparâmetro \(m_{max}\). É criada uma conexão com esses vizinhos, caso o vizinho acabe com mais conexões que \(m_{max}\), eles são re-selecionados utilizando o mesmo método.
def insert(self, key: str, value: list[float]):
max_level = len(self.layers) - 1
level = self._get_level()
while max_level < level:
self._create_layer()
max_level = len(self.layers) - 1
entrypoint: str = self.entrypoint
for level in reversed(range(level, max_level)):
entrypoint, *_ = self.layers[level].search(value, 1, entrypoint)
for level in reversed(range(min(level, max_level) + 1)):
layer = self.layers[level]
layer.add_node(key, value)
if len(layer.nodes) == 1:
self.entrypoint = key
else:
neighbors = layer.select_neighbors_heuristic(
key,
layer.search(value, self.ef_construction, entrypoint),
self.m_max,
)
for neighbor in neighbors:
layer.connect(key, neighbor)
neighbor_neighbors = layer.get_neighbors(neighbor)
m_max = self.m_max0 if level == 0 else self.m_max
if len(neighbor_neighbors) > m_max:
layer.set_neighbors(
neighbor,
layer.select_neighbors_heuristic(
neighbor,
neighbor_neighbors,
m_max,
),
)
Nesse processo de inclusão, existem vários hiperparâmetros que impactam no resultado da estrutura:
-
m_l: constante que altera a probabilidade de gerar uma nova camada. As camadas são necessárias para manter a complexidade \(log(N)\), mas elas ficam ineficientes se existir muita sobreposição de nós entre as camadas. -
m_maxem_max0: indicam a quantidade de conexões que um nó pode ter, om_max0é um valor que se aplica apenas a camada mais inferior. Quanto mais conexões existir, maior a probabilidade de obter o resultado ótimo nas consultas. Por outro lado, um grafo com muitas conexões é mais demorado para navegar e ocupa mais espaço em memória. -
ef_construction: é um parâmetro utilizado no métodoLayer.search, que indica a quantidade de vizinhos a ser retornado pela busca. Quanto mais elementos, mais chances de obter melhores resultados na etapa de conectar os vizinhos, por outro lado demanda mais processamento.
A definição desses parâmetros dependerão da características do conjunto de dados, se tornando um problema muito similar com a escolha de hiperparâmetros para modelos de machine learning.
Escolhendo a vizinhança
O método mais trivial para escolher os vizinhos, é fazer uma simples busca pelos \(m\) mais próximos a partir de uma lista de candidatos:
class Layer:
...
@staticmethod
def distance(x: list[float], y: list[float]) -> float:
return sqrt(sum([(x - y) ** 2 for x, y in zip(x, y)]))
...
def select_neighbors(self, key: str, candidates: list[str], m: int) -> list[str]:
value = self.nodes[key]
best_candidates = sorted(
[
(Layer.distance(v, self.nodes[c]), c)
for v, c in product([value], candidates)
if c != key
],
key=lambda x: x[0],
)
return [c for _, c in best_candidates][:m]
Apesar de funcional, essa implementação ingênua pode criar vizinhanças isoladas, inacessíveis a depender do ponto de entrada da busca. Para mitigar esse cenário, os criadores do algoritmo propuseram uma seleção heurística:
class Layer:
...
@staticmethod
def distance(x: list[float], y: list[float]) -> float:
return sqrt(sum([(x - y) ** 2 for x, y in zip(x, y)]))
...
def select_neighbors_heuristic(
self,
key: str,
candidates: list[str],
m: int,
extend_candidates: bool = True,
keep_pruned_connections: bool = True,
) -> list[str]:
value = self.nodes[key]
neighbors = set([])
working_candidates = set([c for c in candidates if c != key])
if extend_candidates:
for candidate in candidates:
for candidate_neighbor in self.edges[candidate]:
if (
candidate_neighbor not in working_candidates
and candidate_neighbor != key
):
working_candidates.add(candidate_neighbor)
discarded_candidates = set([])
while len(working_candidates) > 0 and len(neighbors) < m:
nearest_wc = self._get_nearest(value, working_candidates)
working_candidates.remove(nearest_wc)
nearest_wc_distance = self.distance(self.nodes[nearest_wc], value)
add_candidate = bool(
sum(
[
nearest_wc_distance < self.distance(value, self.nodes[neighbor])
for neighbor in neighbors
]
)
)
if add_candidate or len(neighbors) == 0:
neighbors.add(nearest_wc)
else:
discarded_candidates.add(nearest_wc)
if keep_pruned_connections:
while len(discarded_candidates) > 0 and len(neighbors) < m:
nearest_candidate = self._get_nearest(value, discarded_candidates)
discarded_candidates.remove(nearest_candidate)
neighbors.add(nearest_candidate)
return list(neighbors)
Se o parâmetro extend_candidates for verdadeiro, a seleção inclui os “vizinhos dos vizinhos” na busca. Com esses candidatos extras, a seleção pode criar conexões entre grupos de vetores que antes ficariam inacessíveis. Se o parâmetro extend_candidates for falso, select_neighbors e select_neighbors_heuristic são o mesmo algoritmo.
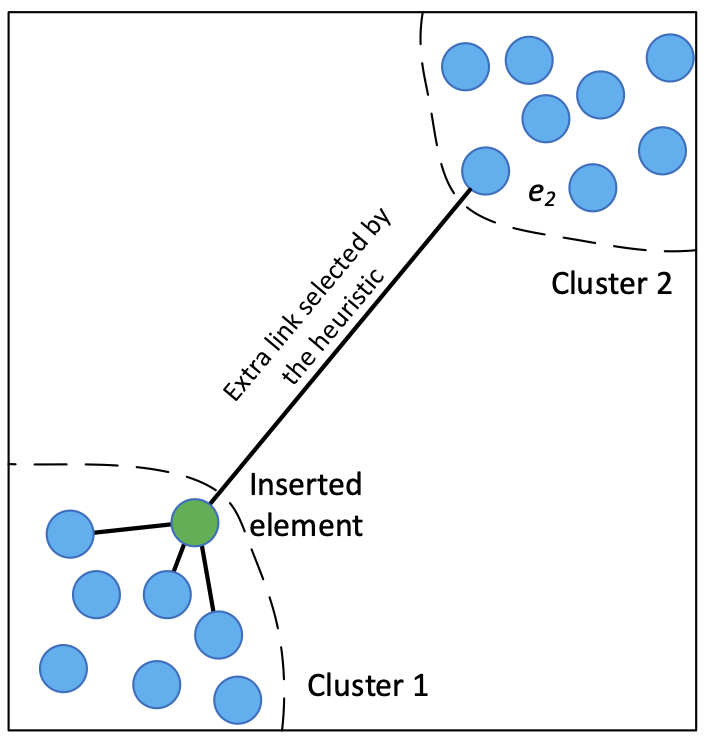
O parâmetro keep_pruned_connections é uma forma de não desprezar conexões válidas, já que a estratégia gulosa de seleção pode acabar descartando vizinhos eleígiveis no meio do caminho.
A busca
A busca é feita a partir da camada superior com menos nós, até chegar a camada inferior que contém todos os nós do conjunto.
class HNSW:
...
def search(
self, query: list[float], k: int, ef_search: int
) -> list[tuple[str, list[float]]]:
if self.entrypoint is None:
return []
entrypoint = self.entrypoint
for layer in reversed(self.layers):
keys = layer.search(query, ef_search, entrypoint)
entrypoint, _ = min(
[(key, Layer.distance(query, layer.nodes[key])) for key in keys],
key=lambda x: x[1],
)
layer, *_ = self.layers
keys = layer.search(query, ef_search, entrypoint)
k_keys = sorted(
[(key, Layer.distance(query, layer.nodes[key])) for key in keys],
key=lambda x: x[1],
)[:k]
return [(key, layer.nodes[key]) for key, _ in k_keys]
...
O parâmetro ef_search indica quantos ítens devem ser considerados: quanto maior esse valor, maior a probabilidade de chegar na solução ótima. Entretanto, o processo de busca é mais caro computacionalmente. O parâmetro k é a quantidade de ítens que devem ser retornados.
A busca em uma camada é um processo guloso, que procura os vizinhos mais próximos a partir de um ponto de entrada. Para evitar ciclos, há uma lista de nós visitados:
class Layer:
...
@staticmethod
def distance(x: list[float], y: list[float]) -> float:
return sqrt(sum([(x - y) ** 2 for x, y in zip(x, y)]))
def _get_nearest(self, query: list[float], nodes: Iterable[str]) -> str:
nearest = ("", sys.float_info.max)
for node in nodes:
node_distance = Layer.distance(query, self.nodes[node])
_, smaller_distance = nearest
if node_distance < smaller_distance:
nearest = (node, node_distance)
return nearest[0]
def _get_furthest(self, query: list[float], nodes: Iterable[str]) -> str:
furthest = ("", -sys.float_info.max)
for node in nodes:
node_distance = Layer.distance(query, self.nodes[node])
_, bigger_distance = furthest
if node_distance > bigger_distance:
furthest = (node, node_distance)
return furthest[0]
...
def search(
self, query: list[float], elements_to_return: int, entrypoint: str
) -> list[str]:
visted = set([entrypoint])
candidates = set([entrypoint])
nearest_neighbors = set([entrypoint])
while len(candidates) > 0:
nearest_node = self._get_nearest(query, candidates)
candidates.remove(nearest_node)
furthest_node = self._get_furthest(query, nearest_neighbors)
if Layer.distance(query, self.nodes[nearest_node]) > Layer.distance(
query, self.nodes[furthest_node]
):
break
for node in self.edges[nearest_node]:
if node not in visted:
visted.add(node)
furthest_element = self._get_furthest(query, nearest_neighbors)
if (
Layer.distance(query, self.nodes[node])
< Layer.distance(query, self.nodes[furthest_element])
or len(nearest_neighbors) < elements_to_return
):
candidates.add(node)
nearest_neighbors.add(node)
if len(nearest_neighbors) > elements_to_return:
nearest_neighbors.remove(furthest_element)
return list(nearest_neighbors)
E como escolher os parâmetros?
Algo que eu sempre digo: se existisse uma forma trivial de escolher os hiperparâmetros, eles seriam constantes e não parâmetros ou escolhidos automaticamente. Eu pensei em explorar esse aspecto nesse post, mas a conclusão é que não devo utilizar essa estrutura para o problema que estou tratando hoje: fazer busca vetorial em pequenos subconjuntos. É mais eficiente filtrar o conjunto com um índice tradicional, para depois ordenar sem uma estrutura adicional como o HNSW.
Eu só pude chegar a essa conclusão, porque entendi como funciona uma busca vetorial. Caso eu precise trabalhar com tunning de um RAG em milhões de registros, já sei quais parâmetros eu devo olhar a depender do problema que estou enfrentando (e.g. tempo de construção, tempo de busca, consumo de memória) e das características dos meus dados. Assim como ajustar os parâmetros de uma random forest por exemplo, é importante realmente entender a dinâmica dos parâmetros do HNSW, para não perder tempo com uma tentiva e erro sem direção.
Eu implementei o algoritmo apenas para fins didáticos, nem tenho certeza de sua corretude, mas é um jeito que me ajuda a realmente entender os problemas. Talvez, eu retome esse assunto de como escolher os parâmetros, mas é um assunto que merece outro post.