Usar árvore ou lista? Sim
Nos últimos tempos, estive estudando sobre banco de dados, acabei encontrando esse ótimo post sobre a arquitetura do Rocks DB1. Achei curioso o uso de skip lists para dados em memória, nunca tinha ouvido falar sobre essa estrutura de dados, mas pareceu promissor: complexidade \(log(n)\) para buscas e manipulação, como uma árvore balanceada, só que mais simples de implementar.
Estudando mais sobre, realmente pareceu simples, aí pensei: será que consigo implementar?
Ao menos falando das mais básicas, sempre achei gostosinho implementar estrutura de dados: são problemas bem definidos, sem dependências externas e normalmente são soluções elegantes.
O que é uma skip list?
A skip list não é composta uma única lista, mas sim múltiplas listas organizadas de forma hierárquica, criando caminhos alternativos para se encontrar uma chave. Uma boa analogia para essa estrutura, são as linhas expressas de uma malha ferroviária.
Em São Paulo temos a Linha 11 da CPTM, que é paralela a Linha 3 do metrô, mas com menos paradas. Usando a linha 11, se alguém quiser ir do Brás para Corinthians-Itaquera, será apenas uma parada no Tatuapé. Usando a Linha 3, serão feitas nove paradas.
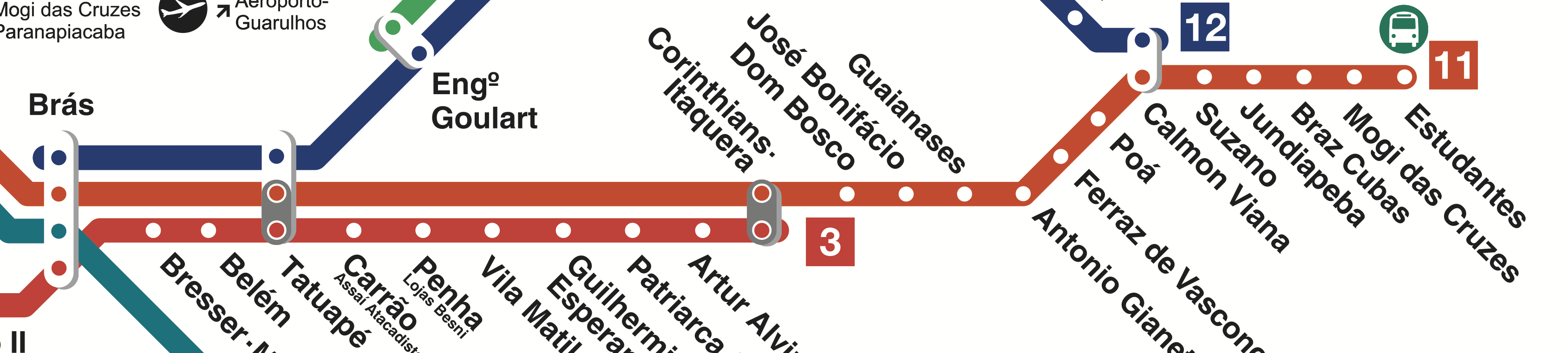
A skip list emula essa estratégia, além da lista principal com todos as chaves, também são criadas “listas expressas” para cortar caminho. As listas de uma skip list são ordenadas, dessa forma é simples ir “baldeando” entre elas.
Abaixo, temos um exemplo de skip list com 4 níveis, contendo os números no intervalo \([0,9]\). Para exemplificar uma busca, vamos procurar pela chave 7 nessa skip list.
--------> 1 --------------------------------------------------> X
--------> 1 --------------------------> 6 --------------> 9 --> X
--------> 1 --------> 3 --------------> 6 --------------> 9 --> X
--> 0 --> 1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9 --> X
Usando as vias expressas da skip list, é possível cortar caminho. Começando pela lista superior, se a chave não for encontrada ou chegar ao fim da lista, faz-se a “baldeação” para a lista inferior.
--> 1
1 --------------------------> 6
6
6 --> 7
Em uma lista ordenada simples, seria necessário visitar todos os nós intermediários, entre o começo da lista e a chave.
--> 0 --> 1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7
Em uma lista ligada comum, seria necessário passar por 7 nós. Utilizando as “linhas expressas”, foi necessário visitar 3 nós para chegar ao valor desejado.
Quem vai pela expressa?
No exemplo anterior, reduziu-se o caminho pela metade, mas nem sempre é o caso. Usando essa outra skip list, que contém as mesmas chaves, mas organizadas de forma diferente.
--------> 1 --> 2 --> 3 --> 4 --> 5 --> 6 --------------> 9 --> X
--> 0 --> 1 --> 2 --> 3 --> 4 --> 5 --> 6 --> 7 --> 8 --> 9 --> X
Ao buscar pela chave 7, reduziria de 7 para 6, o total de nós visitados.
--------> 1 --> 2 --> 3 --> 4 --> 5 --> 6
6 --> 7
Pelo algoritmo de inserção, ambas as listas são válidas, porque a skip list é uma estrutura estocástica: ao inserir uma nova chave na lista, há um sorteio para definir em qual nível ela será incluída.
Esse sorteio é um processo de Bernoulli: jogamos “cara ou coroa”, se for cara, jogamos a moeda novamente. Repete-se esse processo, até dar coroa. Ao final, o nível da chave é definida pela quantidade de caras consecutivas.
Por essa característica aleatória da estrutura, é necessário fazer uma análise estatística da complexidade, considerando o caso médio. No pior caso, a skip list é simplesmente uma lista ligada, mas na média se aproxima de uma árvore de busca binária balanceada.
Esse tipo de análise é bem mais complexa, comparado a simplesmente usar o pior caso como referência. Nesse post, vou abordar apenas a implementação, mas essa aula tem o passo-a-passo de como provar a complexidade \(log(n)\) da skip list.
Implementação
Minha ideia era implementar em Rust – juro que tentei bastante, queria testar algo “real” na linguagem – mas estava tendo muitas dificuldades com a questão de ownership e os ponteiros da lista. A alternativa foi utilizar Go, outra linguagem que parece bem adequada para esse tipo de problema.
Structs
Começando pelas structs, utilizei uma para o nó (Node) e outra para a lista (SkipList). A SkipList contém um array de ponteiros para o início de cada lista, além de marcador para a quantidade de níveis da lista.
type SkipList[K constraints.Ordered] struct {
heads []*Node[K]
levels int
}
A struct Node armazena uma chave. Utilizei campos extras – value e verb – para emular a estrutura de uma memtable do Rocks DB:
key: valor da chave definida como um tipo genérico “comparável”;value: array de bytes contendo o valor;verb: uma enumeração do estado do registro, podendo serPUT,DELouMERGE;nexts: ponteiro para o próximo nó, é um array pois um nó pode estar em múltiplas listas, tendo múltiplos vizinhos.
type Node[K constraints.Ordered] struct {
key K
value []byte
verb base_types.Verb
nexts []*Node[K]
}
Sorteio de nível
Para sortear o nível, é uma função bastante simples: começamos com um nível, sorteamos \({0,1}\). Se der \(1\), um nível é adicionado, caso contrário sai do loop e retorna o nível.
func GetLevel() int {
level := 1
for {
if rand.Intn(2) != 1 {
break
}
level += 1
}
return level
}
Inclusão
O primeiro passo ao incluir um nó, é utilizar a função GetLevel para definir o nível. Caso o level calculado seja maior que o máximo até o momento, o vetor heads da SkipListé estendido para armazenar mais listas.
level := GetLevel()
for {
if level <= this.levels {
break
}
this.levels += 1
this.heads = append(this.heads, nil)
}
O Node é criado com \(N\) vizinhos, sendo \(N\) o nível do nó. Na próxima etapa, esses vizinhos serão atualizados, para o nó ser incluído nas listas.
newNode := Node[K]{
key,
value,
base_types.PUT,
make([]*Node[K], level)}
Após a criação, usamos a lógica da busca para arrumar os ponteiros. Para cada nível, a partir do último, a lista é percorrida até se encontrar a posição correta do nó:
- se for uma lista nova, então o novo nó vira o início;
- se o novo nó é a maior chave da lista, entra no final da lista;
- se o novo nó estiver no meio da lista, deve ser incluído na posição que atenda
b.key < newNode.key < n.key
for i := level - 1; i >= 0; i-- {
if this.heads[i] == nil {
this.heads[i] = &newNode
continue
}
n := this.heads[i]
var b *Node[K]
for {
if n == nil {
b.nexts[i] = &newNode
break
}
if key < n.key {
newNode.nexts[i] = n
if b == nil {
this.heads[i] = &newNode
} else {
b.nexts[i] = &newNode
}
break
}
if key > n.key {
b = n
n = n.nexts[i]
}
}
}
Busca
O processo de busca não é muito diferente da inclusão. Para cada nível, a partir do último, a lista é percorrida e as três possibilidades são tratadas:
- se
key == node.key, retorna o campovalue; - se
key < node.key, desce um nível da lista se for possível, senão retorna erro; - se
key > node.key, vai para o próximo nó da lista. Se o próximo nó for nulo, desce um nível e segue a busca, ou retorna erro caso já esteja no último nível.
func (this *SkipList[K]) Get(key K) ([]byte, error) {
level := this.levels - 1
node := this.heads[level]
befores := this.heads
for {
if node == nil {
return nil, &KeyNotFoundError[K]{Key: key}
}
if node.key == key {
return node.value, nil
}
if key < node.key {
level -= 1
if level < 0 {
return nil, &KeyNotFoundError[K]{Key: key}
}
node = befores[level]
}
if key > node.key {
next_node := node.nexts[level]
if next_node == nil {
level -= 1
if level < 0 {
return nil, &KeyNotFoundError[K]{Key: key}
}
} else {
befores = node.nexts
node = next_node
}
}
}
}
E remoção? E modificação?
Não implementei remoção e modificação, mas a ideia geral não seria tão diferente do processo de inclusão.
Alguns detalhes extras de implementação precisariam ser discutidos – pensando em utilizar a skip list como memtable de Rocks DB – que acredito fazer sentido discutir em outro momento. Por exemplo: faz sentido excluir um nó, se a ideia é ser uma estrutura temporária?
Muito simples
Imaginei que a implementação fosse simples, para inclusão e exclusão, mas não somente isso. Diferente de uma árvore de busca balanceada, não é necessário ficar rebalanceando e tratando múltiplos casos, isso é “delegado” ao sorteio de nível. Achei uma técnica engenhosa, talvez útil para outros problemas.
O que essa característica estocástica simplifica na implementação, complica em termos de análise da complexidade, o que talvez explique skip list não ser um tópico mais comum nas ementas da graduação. Sendo estrutura de dados um tópico contencioso entre programadores, talvez não seja uma boa ideia complicar mais as coisas.