O que é estatística bayesiana?
Eu já ouvi muito se falar sobre um debate entre as abordagens bayesiana e frequentista na estatística, mas a verdade é que nunca entendi as diferenças entre elas. Por isso, decidi fazer o (ótimo) curso Bayesian Statistics: From Concept to Data Analysis1. Ainda não me sinto completamente confortável com os conceitos, mas ajudou bastante a melhorar minha compreensão.
Esse post é a minha tentativa de explicar o conceito, para quem precisa de uma definição maior que uma linha e menor que um curso. Entretanto, ele foi escrito pensando em alguém que já conhece os conceitos da abordagem frequentista como testes de hipótese e máxima verossimilhança.
Conceito
A ideia do paradigma frequentista é que estamos lidando com uma série (hipotética) de eventos infinitos e observamos a frequência relativa dessa sequência de eventos. Um exemplo que se encaixaria bem nessa perspectiva, seria o de estimar a perda de pacotes de um roteador. Acompanhando a quantidade de pacotes perdidos pelo roteador, é intuitivo enxergar os pacotes como uma série infinita e estimar a perda dos mesmos.
Outros problemas não se encaixam tão facilmente nessa premissa. Estimar a proporção de caras e coroas de uma moeda seria razoável – um problema muito parecido com o do roteador inclusive – mas e definir com base nesses lançamentos se uma moeda é honesta?
No paradigma frequentista, temos apenas duas respostas possíveis: \(P(\text{Moeda Honesta}) = \{0,1\}\). Apesar de podermos verificar qual das opções é mais provável com vários lançamentos de moedas, ainda estaremos trabalhando com uma resposta binária para o problema e não uma probabilidade como seria mais intuitivo.
Usando a abordagem bayesiana, podemos interpretar a questão \(P(\text{Moeda Honesta})\) como um palpite em relação a moeda. Duas pessoas, com informações diferentes sobre o problema, podem atribuir probabilidade diferentes a uma mesma moeda por exemplo. No framework bayesiano, consideramos uma probabilidade inicial para a moeda e vamos atualizando-a à medida em que temos mais informações.
Imagino que a diferença entre os métodos continue pouco palpável com essas explicações. Desenvolvendo esse problema da moeda justa – usando ambas as abordagens – acredito que essa diferença de usarmos uma probabilidade associada à moeda faça mais sentido.
Inferência frequentista
Primeiro, vamos observar o problema de definir \(P(\text{Moeda Honesta})\) a partir de uma perspectiva frequentista. A ideia é realizar uma série de \(N\) lançamentos da moeda e inferir a distribuição usando o teorema do limite central.
Vamos supor que foram realizados 100 lançamentos de moeda, resultando em 44 caras e 56 coroas. Para efeitos de notação, vamos definir cara como um [S]ucesso e coroa como [F]racasso. Interpretando esse problema como uma distribuição de Bernoulli, conseguimos chegar a um intervalo do parâmetro \(p\) da distribuição.
\[S = 44 \ F = 56 \\ X_{i} \sim Bernoulli(p) \\ \text{pelo CLT} \ \sum\limits_{i=1}^{100} \sim N(100p, 100p(1-p))\]Lembrando que aproxidamente 95% dos eventos em uma curva normal ficam entre 1,96 desvios-padrão, podemos encontrar o intervalo de confiança da seguinte forma:
\[100p - 1.96\sqrt{100p(1-p)} \ \text{e} \ 100p + 1.96\sqrt{100p(1-p)}\]O valor de \(\hat{p}\) é simplesmente a proporção de caras: \(\hat{p} = \frac{44}{100}\). Substituindo esse valor na equação anterior, temos os seguintes resultados:
\[44 - 1,96\sqrt{44(0.56)} \ \text{e} \ 44 + 1,96\sqrt{44(0.56)} \\ 44 \pm 9.7 = (34.3 , 53.7)\]Por esse intervalo, podemos afirmar com 95% de confiança que a moeda é justa. Isso significa que – se repetirmos esse experimento indefinidamente – 95% das vezes a média estará dentro do intervalo gerado usando os cálculos descritos acima.
Não é exatamente uma resposta direta e clara para o problema, não temos aqui uma probabilidade da moeda ser honesta ou desonesta. Vejamos agora, como a inferência bayesiana pode nos ajudar a obter uma resposta mais clara ao problema da moeda.
Inferência Bayesiana
A inferência bayesiana nos ajuda a modelar melhor esse problema com os conceitos de distribuição a priori e a posteriori. No caso de nossa moeda, a distribuição a priori é referente a informação inicial que temos da moeda. Ou seja, o nosso palpite antes de observar qualquer experimento. A distribuição a posteriori considera o nosso palpite a priori, mais a informação obtida com os experimentos.
É um modelo bem intuitivo: temos um palpite inicial em relação ao valor de \(P(\text{Moeda Honesta})\) e vamos atualizando ele à medida em que fazemos os experimentos.
Na abordagem frequentista, não temos a ideia do palpite inicial, pois a intepretação é que a “honestidade” da moeda é uma característica física…como se encontrar a distribuição fosse um processo similar a medir o diâmetro dela.
Simplificando a questão
Antes de abordar o problema original, vamos trabalhar com uma versão simplificada dele. Suponha que fizemos 5 lançamentos de moeda e temos apenas duas distribuições candidatas, ao invés de termos uma distribuição honesta e infinitas outras “desonestas”. Nesse caso, temos o seguinte problema23 na abordagem frequentista:
\[\theta = \{\text{honesta}, \text{desonesta}\} \\ X \sim Bin(5, ?) \\ f(x \mid \theta) = \begin{cases} {5\choose x} \frac{1}{2}^5 \ \text{se} \ \theta = \text{honesta} \\ {5\choose x} (0.7)^x(0.3)^{(5-x)} \ \text{se} \ \theta = \text{desonesta} \end{cases} \\ = {5\choose x} \frac{1}{2}^5 I_{\{\theta = \text{honesta}\}} + {5\choose x} (0.7)^x(0.3)^{(5-x)} I_{\{\theta = \text{desonesta}\}}\]De acordo com a definição acima, estamos considerando 5 lançamentos de moeda. Se \(\theta = honesta\), esperamos que o parâmetro \(?\) (a probabilidade \(p\) da distribuição binomial) seja igual a \(\frac{1}{2}\). Por outro lado, se \(\theta = desonesta\), estamos esperando que o parâmetro \(?\) seja igual a \(0.7\).
Supondo que tivemos 2 sucessos em 5 lançamentos, podemos usar \(x = 2\) para calcular a máxima verosssimilhança e inferir qual das duas distribuições é a mais provável:
\[f(\theta \mid 2) = \begin{cases} {5\choose 2} \frac{1}{2}^5 = 0.3125 \ \text{se} \ \theta = \text{honesta} \\ {5\choose 2} (0.7)^2(0.3)^{(5-2)} = 0.1323 \ \text{se} \ \theta = \text{desonesta} \end{cases} \\\]A partir da comparação entre as duas distribuições, podemos inferir que esses resultados são mais prováveis partindo de uma moeda honesta do que desonesta. Entretanto, não há uma resposta da probabilidade das duas distribuições candidatas.
Sabemos que \(f(\theta=honesta \mid x=2) > f(\theta=desonesta \mid x=2)\), mas não sabemos o valor da probabilidade \(f(\theta=honesta \mid x=2)\). Lembre-se: o paradigma frequentista não considera \(P(\theta=honesta)\) como uma probabilidade, já que nessa abordagem essa questão é tratada como uma grande física no qual só temos dois valores possíveis \(\{0,1\}\).
Bayes ao resgate
Usando a abordagem bayesiana, conseguimos uma estimativa de \(f(\theta=honesta \mid x=2)\), trazendo assim uma resposta mais informativa e direta para o problema proposto.
Para começar, precisamos definir o nosso palpite inicial (a priori): vamos considerar \(P(\text{desonesta}) = 0.6\). Isso significa que – antes de qualquer experimento – entendemos que essa moeda tem uma chance ligeiramente maior de ser desonesta do que honesta.
Transformando o problema de máxima verossilhança para incluir a probabilidade a priori, chegamos a seguinte formulação do problema usando o teorema de Bayes:
\[f(\theta \mid x) = \frac{f(x \mid \theta)f(\theta)}{\sum_{\theta} f(x \mid \theta)f(\theta)}\]Representando o nosso problema nessa nova formulação:
Na parte superior da equação, temos o mesmo cálculo usado na inferência anterior condicionado às probabilidade a priori de cada uma das hipóteses de distribuição: \(P(\text{honesta}) = 0.4\) e \(P(\text{desonesta}) = 0.6\). Na parte inferior, temos uma constante de normalização que considera a soma de todas as distribuições candidatas.
Usando os mesmos resultados de experimentos, conseguimos estimar \(f(\theta=honesta \mid x=2)\):
Com isso, temos uma resposta para \(P(\theta=honesta \mid x=2)\) que é \(.612\).
Perceba que, usando a abordagem bayesiana, temos uma resposta muito mais clara e informativa para o problema, que é a probabilide da moeda ser honesta.
Um porém, que pode incomodar alguns, é a questão de precisar definir uma probabilidade a priori de forma subjetiva. O que é um ponto compreensível, já que lidar com a priori é uma das questões filosóficas dos métodos bayesianos.
Independente dessa (complicada) questão de trabalhar com distribuições a priori, acredito que já seja possível ter uma visão mais clara de quais as diferenças práticas e conceituais entre as duas abordagens.
Voltando à questão original
Para introduzir a diferença entre uma solução bayesiana e frequentista, usamos uma simplificação do problema original considerando apenas duas distribuições candidatas. Em um caso real, é mais provável que precisemos inferir \(P(\theta=honesta)\), sem definir qual seria a distribuição desonesta. Para esse caso mais genérico, precisamos considerar as infinitas distribuições possíveis para uma moeda e trabalhar com o problema de forma contínua.
Assumindo agora que nosso palpite sobre a moeda é “neutro”, usaremos uma distribuição a priori uniforme. Ou seja, consideramos que todos os valores do parâmetro \(p\) da distribuição binomial são equiprováveis.
Para trabalhar com essa abordagem, precisamos de versão contínua do teorema de bayes, já que estamos trabalhando agora com infinitas possibilidades e não somente duas.
A nova formulação continua seguindo a estrutura \(\frac{\text{a posteriori} \ * \ \text{a priori}}{\text{constante de normalização}}\), a diferença é que agora precisamos trabalhar com uma integral no lugar do somatório na constante de normalização, já que estamos lidando com um problema contínuo agora.
Assumindo que \(\theta \sim U[0,1]\), podemos considerar que \(f(\theta) = I_{\{0 \leq \theta \leq 1\}}\). A distribuição a posteriori continua seguindo uma binomial, logo temos que \(f(\theta \mid y) = \theta^y(1-0)^{(n-y)}\).
Para \(Y= 1\) em um lançamento, conseguimos calcular facilmente a distribuição resultante já que temos um cálculo trivial da integral:
Antes de qualquer experimento, tínhamos uma distribuição a priori uniforme. Depois do primeiro experimento, a distribuição a posteriori foi atualizada para \(2\theta \ I_{\{0 \leq \theta \leq 1\}}\).
Se realizarmos mais experimentos – e eles retornarem sempre sucesso – observe que a distribuição do valor de \(\theta\) vai se adensando próximo de 1, conforme esperado para uma moeda que sempre retorna sucesso.
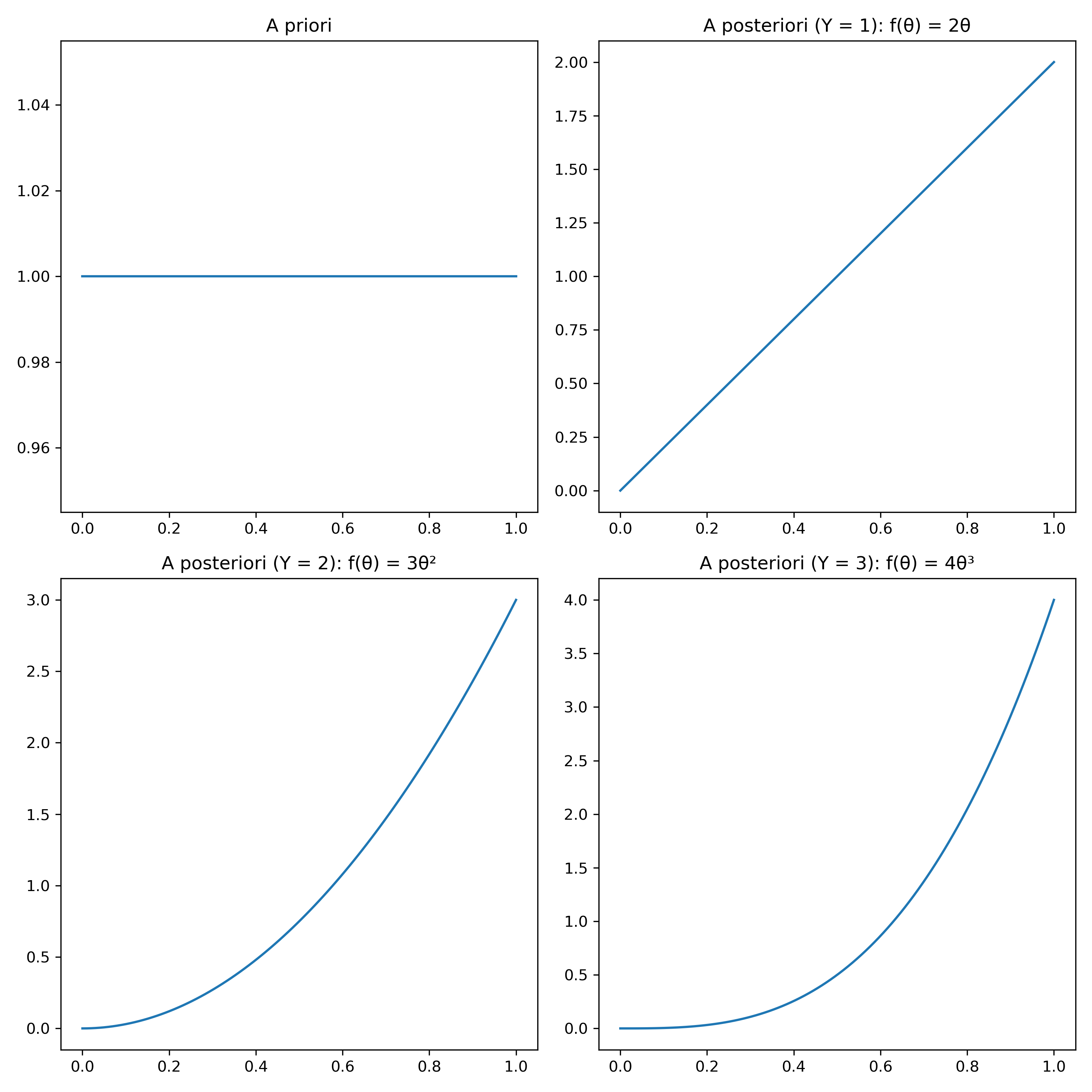
Ao final, a posteriori é uma função de densidade de \(\theta\), que indica o parâmetro da distribuição da moeda \(X\): \(X_{i} \sim Bernoulli(\theta)\).
Essa função nos possibilita calcular os intervalos de probabilidade de \(\theta\), assim como faríamos com qualquer problema envolvendo uma função de densidade. Podemos calcular \(P(\theta > 0.5)\) por exemplo, para verificar a probabilidade da moeda ser enviesada para resultar em mais caras. Considerando apenas a distribuição a priori, temos que \(P(\theta > 0.5) = 0.5\). Para a posteriori, definida com a observação \(Y=1\), essa probabilidade aumenta para \(P(\theta \mid Y=1) = 0.75\).
A abordagem bayesiana é mais complexa de se modelar, mas ao obtermos uma distribuição de \(\theta\) conseguimos trabalhar de forma muito mais claras as perguntas originais do problema. A partir dessa distribuição, podemos trabalhar com várias hipóteses diferentes aplicando o conceito de intervalo de confiança. Na abordagem frequentista, precisamos lidar com a ideia dos infinitos experimentos que fornece uma resposta pouco intuitiva para a questão original.
Conclusão
Espero que esse pequeno exemplo tenha ajudado a entender qual a diferença conceitual entre as duas abordagens, como temos uma resposta mais intuitiva para o problema da moeda ao abordá-lo pela perspectiva bayesiana. Mas que, apesar dessa vantagem interpretativa, modelar os problemas dessa forma é mais difícil como já podemos perceber nesse exemplo e só piora para casos mais complexos.
Além disso, temos o elefante na sala que é a definição da distribuição a priori, mas isso é uma discussão que não me aprofundei pois estaria bem acima do meu conhecimento atual. Intuitivamente, faz sentido para mim trabalhar dessa forma, especialmente se utilizarmos mecanismos como a priori não informativa que procuram priorizar as informação obtida pelos experimentos em detrimento a priori.
Minha expectativa ao fazer o curso não era aplicar estatística bayesiana de imediato, mas finalmente entender o conceito e mapear onde pode ser útil futuramente. Nesse contexto, o curso me atendeu plenamente e recomendo para quem continua achando vaga essa discussão mesmo após chegar ao final desse post.
-
Muitos cursos do Coursera fazem parte de uma graduação, que tem acesso liberado por uma mensalidade. Esse é um curso isolado, o acesso a todo conteúdo e tarefas é gratuito, sendo necessário pagar apenas pelo certificado se for desejável. ↩
-
perceba que estamos usando a notação \(f(x \mid \theta)\) ao invés de \(P(x \mid \theta)\) porque – segundo o curso – é mais comum usar essa notação em estatística bayesiana. ↩
-
A função \(I_{\{\text{condição}\}}\) é chamada de função indicadora. Ela é apenas uma forma de escrever funções condicionais usando multiplicadore de 0 e 1. ↩