LSTM para séries temporais
Problemas que envolvem predições de séries temporais são comuns em várias áreas de negócios (e.g. previsão de demanda, acompanhamento de preços, evolução de carteira) e, geralmente, não exigem trabalho de rotulação para serem utilizados em algoritmos de predição. Por outro lado, não são muito fáceis de serem modelados.
Se optarmos por métodos autoregressivos, não é trivial adicionar variáveis exógenas a série nesse tipo de estratégia. Interpretando a série como um problema de regressão, é mais simples adicionar variáveis exógenas, mas é mais complicado mapear características importantes como sazonalidade e tendência, inerentes ao conceito de série temporal.
Nesse contexto de trade-offs entre técnicas de regressão e de séries temporais, as redes neurais recorrentes aparecem como uma boa alternativa, que ataca as limitações das duas estratégias. As RNNs têm capacidade de trabalhar com diversas variáveis para prever a série e também apresentam mecanismos para capturar características de ciclos e sazonalidades da série.
Nesse post, será apresentada o uso de uma LSTM para o problema de prever o volume de aluguéis de bicicletas em um serviço de compartilhamento, ilustrando o uso de redes neurais em problemas de séries temporais.
Bike Sharing Dataset
O dataset utilizado nesse post é o Bike Sharing Dataset, que contém o histórico de 2 anos de um serviço de compartilhamento de bicicletas. Além do volume de bicicletas alugadas de hora em hora, esse dataset também contém informações das condições do tempo (temperatura, humidade e chuva/neve).
Abaixo, a descrição das variáveis fornecida pelo criador do dataset.
1. instant: record index
2. dteday : date
3. season : season (1:springer, 2:summer, 3:fall, 4:winter)
4. yr : year (0: 2011, 1:2012)
5. mnth : month ( 1 to 12)
6. hr : hour (0 to 23)
7. holiday : weather day is holiday or not (extracted from http://dchr.dc.gov/page/holiday-schedule)
8. weekday : day of the week
9. workingday : if day is neither weekend nor holiday is 1, otherwise is 0.
10. weathersit :
* 1: Clear, Few clouds, Partly cloudy, Partly cloudy
* 2: Mist + Cloudy, Mist + Broken clouds, Mist + Few clouds, Mist
* 3: Light Snow, Light Rain + Thunderstorm + Scattered clouds, Light Rain + Scattered clouds
* 4: Heavy Rain + Ice Pallets + Thunderstorm + Mist, Snow + Fog
1. temp : Normalized temperature in Celsius. The values are divided to 41 (max)
2. atemp: Normalized feeling temperature in Celsius. The values are divided to 50 (max)
3. hum: Normalized humidity. The values are divided to 100 (max)
4. windspeed: Normalized wind speed. The values are divided to 67 (max)
5. casual: count of casual users
6. registered: count of registered users
7. cnt: count of total rental bikes including both casual and registered
O nosso objetivo é projetar o valor de cnt, de hora em hora, com base em todas essas variáveis e o comportamento histórico da série. Para entender se essas variáveis adicionais de clima são importantes para entender a série, vamos fazer uma breve análise exploratória do dataset.
Análise Exploratória
Na própria descrição do dataset, o criador diz que as variáveis de clima impactam no comportamento da série, vamos plotar alguns gráficos para verificar como funcionam essas relações.
Iniciando a análise no nível diário, vamos entender como se comportam os diferentes dias da semana no dataset, selecionando um mês e um dia da semana para análise.
Na figura 1, temos os sábados do mês de Outubro de 2011, em que podemos ver os impactos de um dia muito frio. O volume do aluguel de bicicletas ficou bastante abaixo no sábado do dia 2011-10-29, comparado a outros sábados do mesmo mês com temperaturas mais agradáveis.
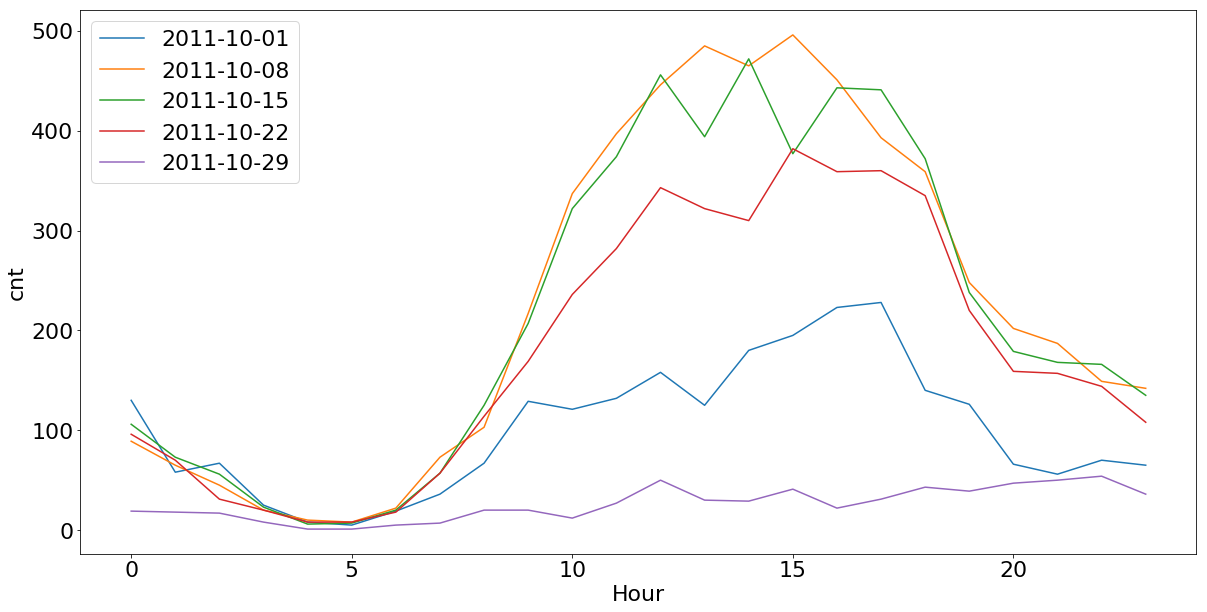
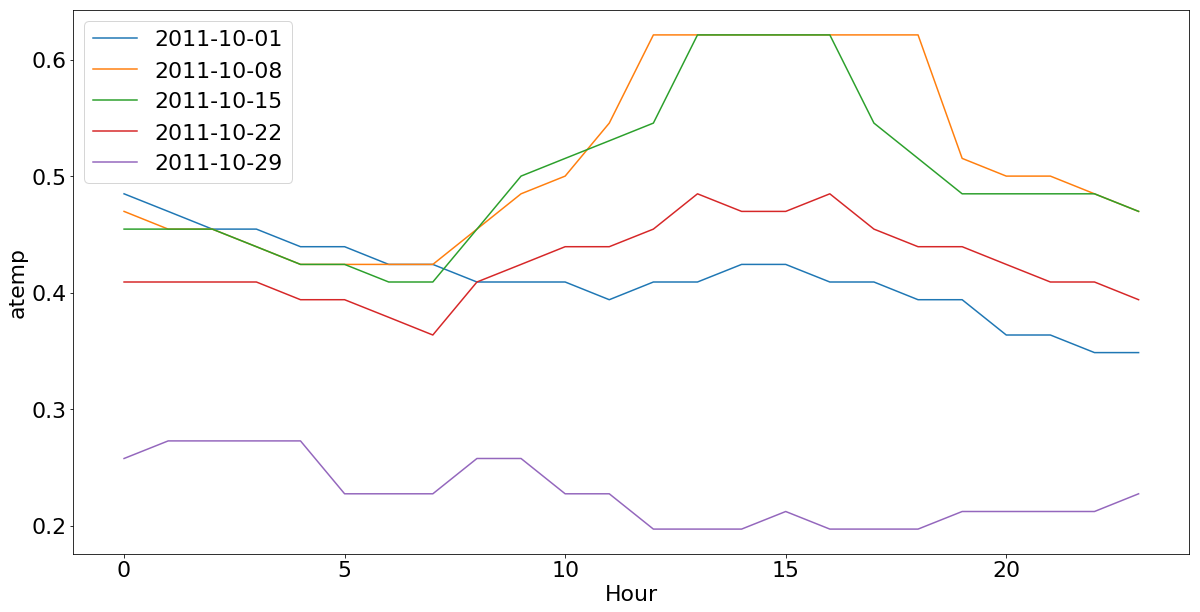
Na figura 2, podemos ver um exemplo do efeito inverso do observado em Outubro. Uma quinta-feira muito quente no mês de de Junho (2011-06-09), em que também tivemos um volume menor de aluguéis, comparado a outras quintas-feiras do mesmo mês com temperaturas mais agradáveis.

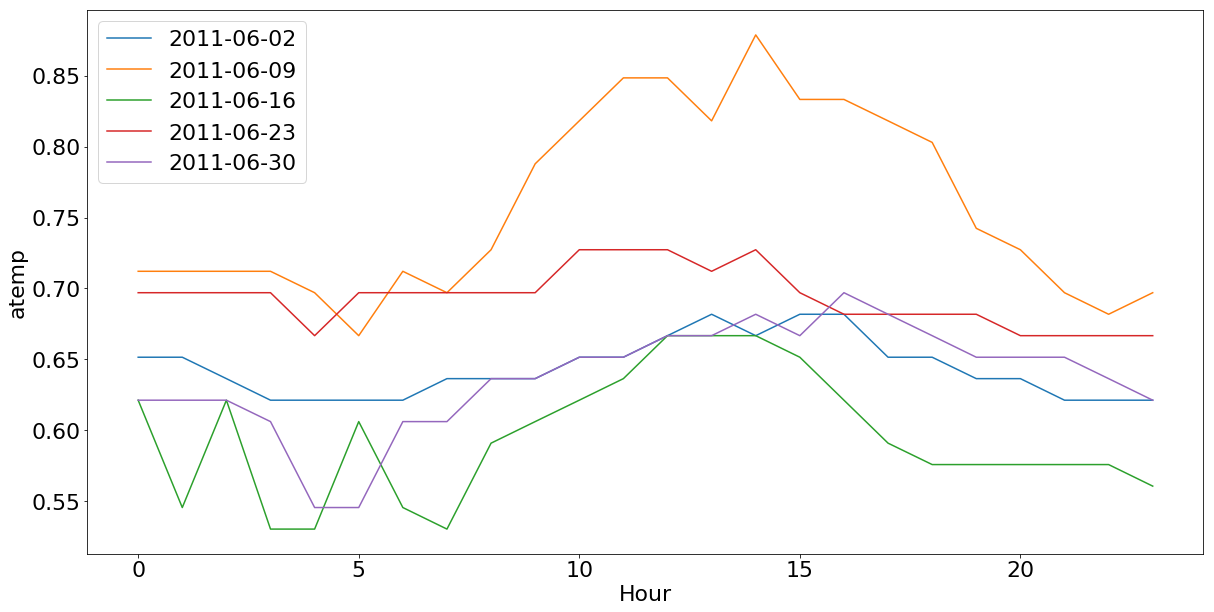
Além da questão das temperaturas extremas, é interessante notar a diferença da curva entre as quintas-feiras e os sábados. Nas quintas, os picos de aluguéis estão nos horários de chegada e saída do trabalho, enquanto nos sábados o pico é no horário da tarde.
Partindo para um visão anual, mais ampla, podemos ver que a temperatura maior tem um impacto positivo no aluguel de bicicletas, como mostrado na figura 3, que apresenta o agregado de aluguéis e temperaturas diários no ano de 2011.

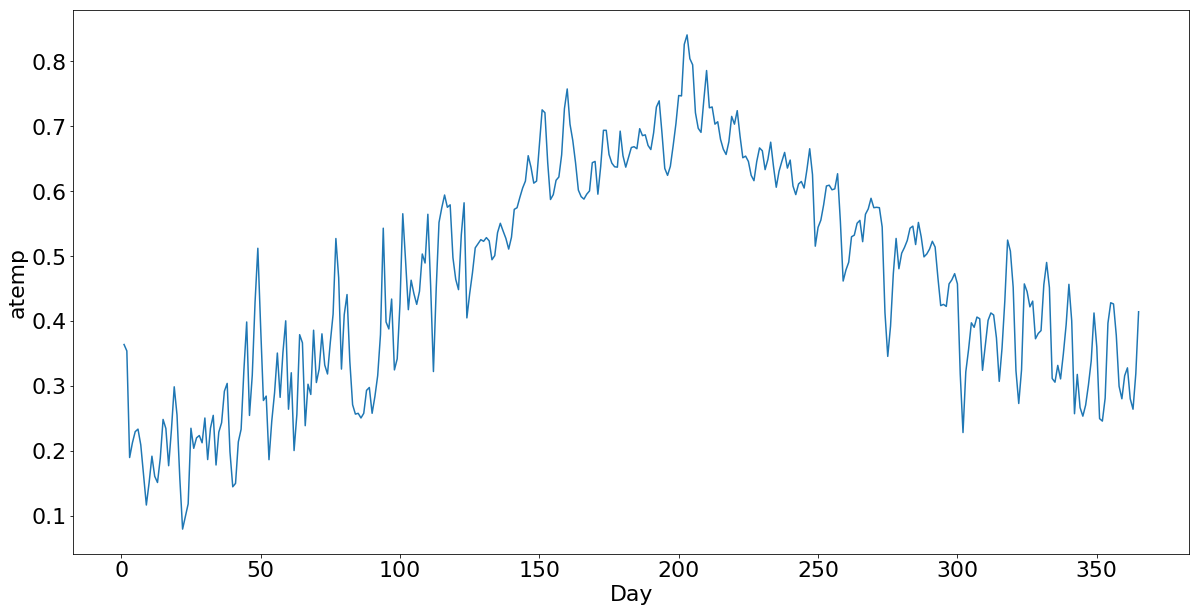
Expandindo essa análise para o ano de 2012, além desse ciclo anual das temperaturas do ano, podemos observar que há uma tendência de crescimento de 2011 para 2012 no uso do serviço como um todo (Figura 4).
Por esses gráficos, podemos entender que a temperatura é uma variável importante para estimar o volume de bicicletas alugadas. Os dias com temperaturas extremas parecem menos convidativos ao uso de bicicletas e, de uma perspectiva geral, o calor parece incentivar o aluguel de bicicletas.
Além da temperatura, outras características como a indicação de dia chuvoso, nublado ou com neve também parecem relevantes para o modelo. No boxplot da Figura 5, podemos ver como chuva e neve impactam negativamente no aluguel de bicicletas, enquanto dias abertos tem um efeito positivo.

A partir dessa breve análise 1, podemos perceber que as condições climáticas são um fator relevante para estimar o volume de aluguéis de bicicletas. Seria temerário modelar um preditor somente com o comportamento da série, sem considerar as variáveis de clima, mas também é visível que temos características inerentemente temporais como os ciclos diários e a tendência de crescimento do serviço ao longo do tempo.
RNNs para séries temporais
O problema de prever o número de bicicletas alugadas envolve tanto questões sazonais (dia da semana e estações do ano) como variáveis exógenas (temperatura e chuva/neve). Nessa seção, iremos entender o porquê das redes neurais serem uma opção adequada para esse tipo de problema, já que elas têm o poder de incorporar ambas características do problema.
RNN
As redes neurais recorrentes são bastante utilizadas para problemas com dados sequenciais não estruturados, como processamento de linguagem natural e reconhecimento de fala, mas suas características são interessantes para qualquer problema com caráter de sequência – como é o nosso caso.
As RNNs têm uma arquitetura básica como a da figura 6, na qual a informação computada em \(t\) é utilizada para calcular \(t + 1\).
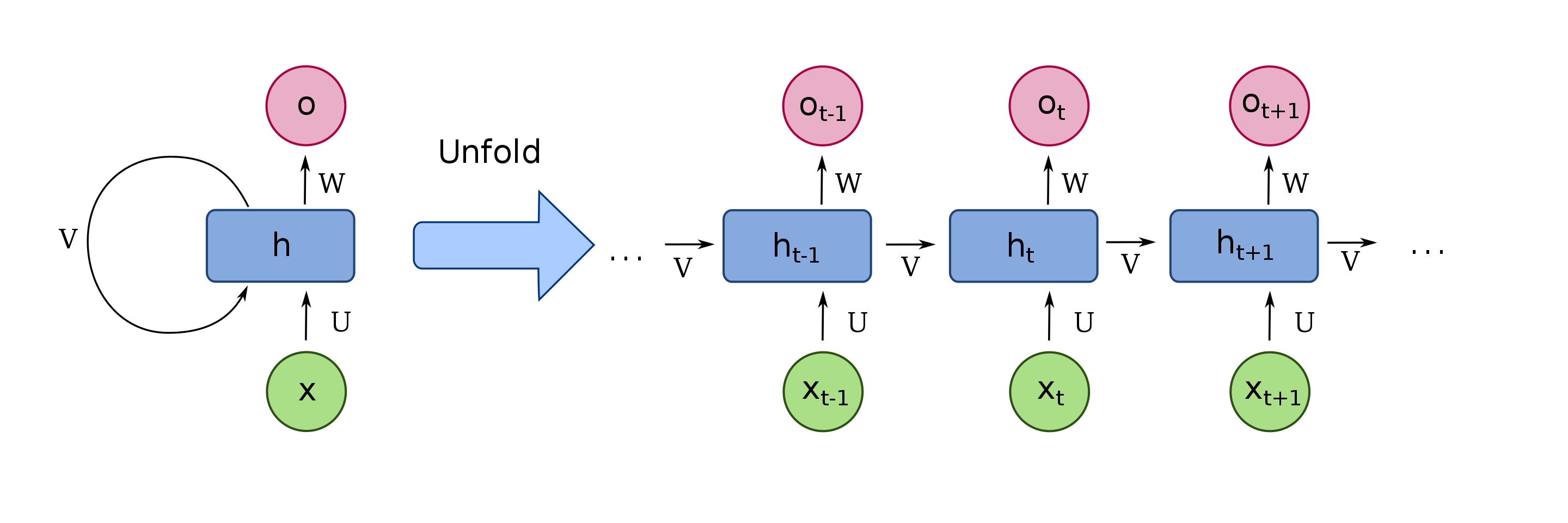
No momento \(t\), a rede computa \(V_{t}\) e \(W_{t}\), essas saídas são calculadas com base nas caraterísticas da posição atual (\(X_{t}\)) e na saída do passo anterior (\(V_{t-1}\)).
\[V_{t} = g(W_{vv}V_{t-1} + W_{vx}X_{t} + b_{a}) \\ W_{t} = g(W_{ov}V_{t} + b_{o})\]A função de ativação \(g(x)\) é normalmente uma \(tanh\), mas nada impede de ser utilizada outra função de ativação para calcular \(V_{t}\) e \(W_{t}\).
Depois de calculado \(W_{t}\), esse vetor de saída pode ser conectado a uma camada final, que pode ser uma softmax para problemas de classificação ou até mesmo uma outra rede neural. Para o nosso caso, em que queremos estimar o total de aluguéis, a saída \(W_{t}\) será conectada a uma camada linear \(O_{t}\) com um neurônio na saída, que retornará o valor da projeção feita pela rede.
Essa á a arquitetura mais básica de uma RNN, soluções mais complexas como a GRU e LSTM, adicionam o conceito de portões a esse desenho, que controlam a passagem de informação entre as etapas da sequência.
LSTM
As LSTM é umas das arquiteturas de RNNs mais populares, muito usada na área de NLP. Como podemos ver na sua arquitetura (Figura 7), é uma rede que possui bastante componentes adicionais em comparação a uma RNN simples.
Esses componentes são os chamados gates (portões), sua função é controlar a passagem de informação entre as etapas da rede, não limitando a “memória” apenas a etapa imediatamente anterior. Dessa forma, a rede neural pode aprender com informações de etapas muito anteriores que podem influenciar na predição da etapa atual da série – parecido com a ideia dos métodos autogressivos para séries temporais.
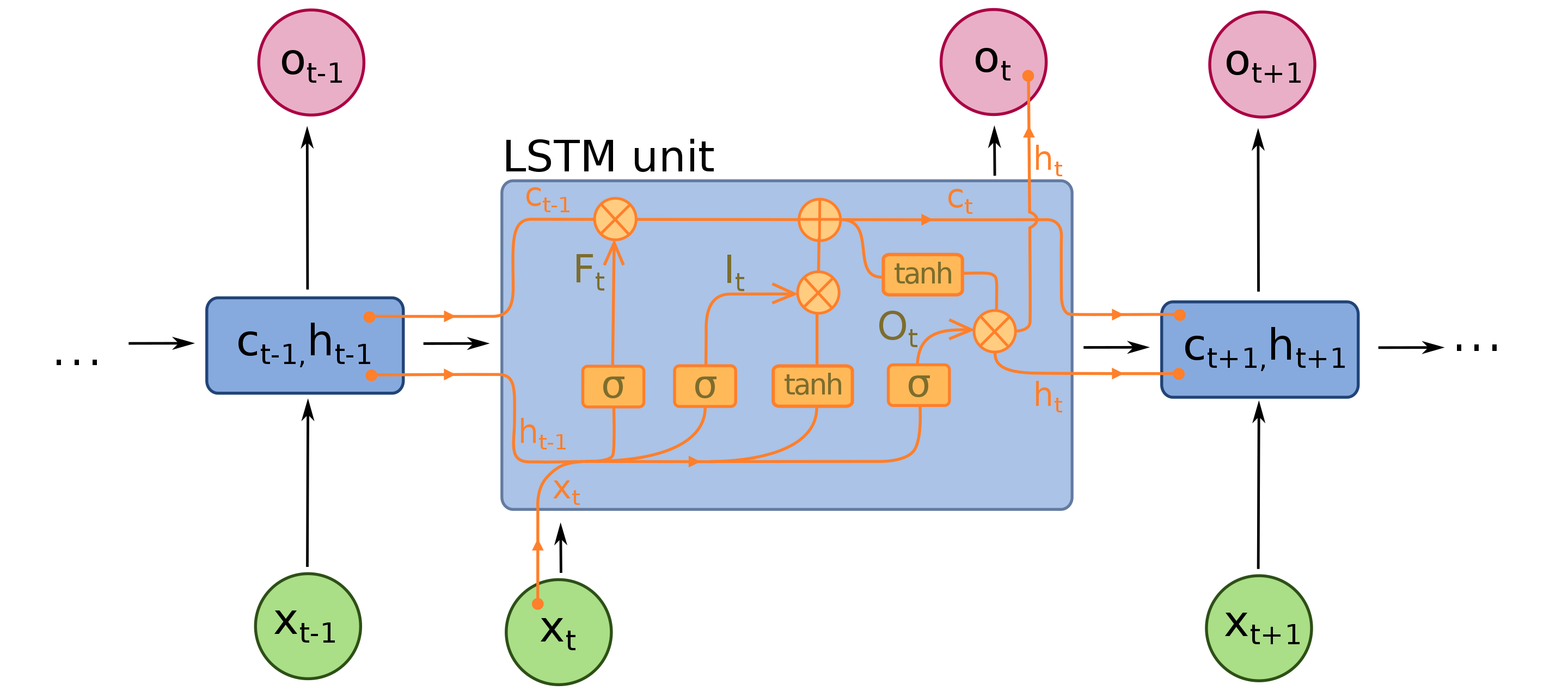
Esses gates são aplicados na entrada/saída da rede, como um vetor de “máscara”, com valores entre 0 e 1, que indicam o quanto de informação deve ser propagada. É bem similar ao Dropout 2 em sua forma de funcionamento, mas com essa “máscara” aprendida pela rede para reaproveitar informações da série, ao invés de ser definida aleatoriamente durante o treinamento.
Gates (portões)
A LSTM utiliza três portões diferentes: forget gate, input gate e output gate.
\(F_{t} = \sigma(W_{fa}a_{t-1} + W_{fx}x_{t} + b_{f})\): chamado de forget gate, responsável por definir o que deve ser ignorado das entradas da etapa atual.
\(I_{t} = \sigma(W_{ia}a_{t-1} + W_{ix}x_{t} + b_{i})\): chamado de input gate, responsável por definir o que deve ser propagado da etapa anterior.
\(O_{t} = \sigma(W_{oa}a_{t-1} + W_{ox}x_{t} + b_{l})\): chamado de output gate, responsável por definir o que deve ser passado da etapa atual para a próxima.
Os portões \(F_{t}\) e \(I_{t}\) são aplicados de forma a combinar \(\widetilde{c}_{t}\) e \(c_{t-1}\) para chegar na saída \(c_{t}\), enquanto o portão \(O_{t}\) é aplicado na saída da rede \(h_{t}\).
\[\widetilde{c} = tanh(W_{ca}a_{t-1} + W_{xa}x_{t} + b_{c}) \\ c_{t} = F_{t} \ast \widetilde{c} + I_{t} \ast c_{t-1} \\ h_{t} = O_{t} \ast tanh(c_{t})\]A função sigmoide \(\sigma\) usada nos portões podem ter qualquer valor entre 0 e 1, mas é comum que elas acabam com valores muito próximo dos extremos, funcionando como um filtro binário do tipo “passa” ou “não passa” informação adiante.
São esses portões que ajudam a rede a mapear características temporais do problema, é possível que algum valor de \(c_{0}\) seja propagado para várias etapas posteriores, sendo utilizados quando a rede achar “pertinente” e ir posteriormente “esquecendo” essa informação quando necessário.
Utilizando a LSTM
As redes LSTM são complexas de entender, mas simples de usar. A arquitetura “fixa” e poucos parâmetros as tornam muito prática de serem utilizadas com o Keras. Com poucas linhas de código, é possível treinar uma rede para projetar os valores de uma série temporal. Nessa seção, será explicado o passo a passo para criar uma LSTM para o nosso dataset.
Preparação dos dados
As variáveis contínuas desse dataset, como temperatura e humidade do ar, já estão em uma escala entre 0 e 1, mas ainda é necessário tratar os dados categóricos. Abaixo, o código feito para carregar o dataset como um dataframe e transformar as variáveis categóricas para uma representação one-hot-encoding.
import pandas as pd
def load_dataset():
ds = pd.read_csv('resources/hour.csv')
ds['dteday'] = pd.to_datetime(ds['dteday'])
return ds
def one_hot_encoding(df, field):
one_hot_encoded = pd.get_dummies(df[field])
return pd.concat([df.drop(field, axis=1), one_hot_encoded], axis=1)
def preprocess_dataset(df):
df_reduced = df[['dteday', 'cnt', 'season','yr', 'mnth','hr', 'holiday', 'weekday', 'workingday', 'weathersit', 'temp', 'atemp', 'hum', 'windspeed']]
df_reduced = one_hot_encoding(df_reduced, 'season')
df_reduced = one_hot_encoding(df_reduced, 'mnth')
df_reduced = one_hot_encoding(df_reduced, 'hr')
df_reduced = one_hot_encoding(df_reduced, 'weekday')
df_reduced = one_hot_encoding(df_reduced, 'weathersit')
return df_reduced
dataset = load_dataset()
dataset = preprocess_dataset(dataset)
Note que variáveis periódicas, como mnth e hr, também foram transformadas em one-hot-encoding. Apenas escalar as variáveis periódicas entre 0 e 1, como se fossem variáveis ordinais, fez com que a rede não conseguisse convergir, mesmo com várias épocas de treinamento.
Treinamento e validação
O problema que estamos lidando é de séries temporais, então não faz sentido amostrar aleatoriamente para dividir o dataset entre treino e validação, como seria o caso para um problema de regressão ou classificação. Os dados de treino precisam ser contíguos e estar antes no tempo que os dados de validação.
Seguindo uma estratégia comum em deep learning, vamos separar o conjunto de dados como treino, desenvolvimento e validação. O conjunto de treino e desenvolvimento serão usadas na etapa de treinamento, para “tunar” os parâmetros de rede e do treinamento. O conjunto de validação será apenas para verificação final após treinamento da rede.
Serão usados os dados até Outubro de 2012 para treinamento, o mês de Novembro de 2012 como conjunto de desenvolvimento e o mês de Dezembro de 2012 como validação.
- Treino: 2011-01-01 até 2012-10-31
- Desenvolvimento: 2012-11-01 até 2012-11-30
- Validação: 2012-12-01 até 2012-12-31
Abaixo, o código para separação do dataframe entre treino, desenvolvimento e validação
from datetime import datetime
def filter_by_date(ds, start_date, end_date):
start_date_parsed = datetime.strptime(start_date, "%Y-%m-%d")
start_end_parsed = datetime.strptime(end_date, "%Y-%m-%d")
return ds[(ds['dteday'] >= start_date_parsed) & (ds['dteday'] <= start_end_parsed)]
train = filter_by_date(dataset, '2011-01-01', '2012-10-31')
dev = filter_by_date(dataset, '2012-11-01', '2012-11-30')
val = filter_by_date(dataset, '2012-11-01', '2012-12-31')
Após separar os conjuntos, podemos transforma-los em vetores numpy para serem usados na rede neural. Perceba que o reshape do vetor de entrada é no formato (# de linhas, 1, # de variáveis) ao invés de (# de linhas, # de variáveis).
O dado de entrada precisa ser formatado assim, pois a segunda dimensão se refere ao comprimento da sequência. Em nosso caso, o valor é 1 pois cada etapa da sequência gera uma saída. Para alguns problemas, ao invés de gerar uma saída por etapa da sequência, geramos apenas uma saída final para a sequência toda.
import numpy as np
def reshape_dataset(ds):
Y = ds['cnt'].values
ds_values = ds.drop(['dteday', 'cnt'], axis=1).values
X = np.reshape(ds_values, (ds_values.shape[0], 1, ds_values.shape[1]))
return X, Y
X_train, Y_train = reshape_dataset(train)
X_dev, Y_dev = reshape_dataset(dev)
X_val, Y_val = reshape_dataset(val)
Por fim, é útil criar um callback do Keras para vermos o gráfico de evolução de treinamento em tempo real, isso é bastante útil para fazer o ajuste dos parâmetros.
%matplotlib inline
import keras
from matplotlib import pyplot as plt
from IPython.display import clear_output
class PlotLosses(keras.callbacks.Callback):
def on_train_begin(self, logs={}):
self.i = 0
self.x = []
self.losses = []
self.val_losses = []
self.fig = plt.figure()
self.logs = []
def on_epoch_end(self, epoch, logs={}):
self.logs.append(logs)
self.x.append(self.i)
self.losses.append(logs.get('loss'))
self.val_losses.append(logs.get('val_loss'))
self.i += 1
clear_output(wait=True)
plt.plot(self.x, self.losses, label="loss")
plt.plot(self.x, self.val_losses, label="val_loss")
plt.legend()
plt.show()
plot_losses = PlotLosses()
LSTM no Keras
O uso da LSTM no Keras é bastante simples, bastando ao usuário definir a dimensão do vetor de entrada, a quantidade de neurônios e a função de saída. O vetor de entrada, após as transformações de variáveis, tem 58 dimensões. A quantidade de neurônios, após alguns testes, foi definida como 200 que alcançou o mesmo fit de redes maiores sem onerar tanto a perfomance do treinamento. Por fim, a saída será uma camada com um único output com o valor estimado dos aluguéis.
Adicionei uma camada de Dropout entre a saída da rede (\(W_{t}\)) e a saída final (\(O_{t}\)), procurando mitigar problemas de sobreajuste. Não utilizei essa técnica nas camadas internas da rede, pois elas acabavam atrasando muito o aprendizado, mas o ideal seria entender melhor o uso de dropout nas camadas internas da LSTM.
O otimizador utilizado foi o Adam, que geralmente é o mais rápido e estável para convergir. Após experimentos, percebi que o valor padrão da taxa de aprendizado (0,001) era muito baixo. Subindo para 0,01 a taxa de aprendizado, a convergência ficou muito mais rápida e também alcançou taxas de erros menores. Combinando esse aumento de taxa de aprendizado com uma taxa de decaimento de 0,001, a rede consegue aprender rapidamente e continuar convergindo na parte do ajuste fino.
A rede está usando como função de perda a métrica de erro absoluto médio, dessa forma temos uma visão clara de quanto estamos errando comparado ao valor absoluto das predições. Abaixo, o código completo para definição da LSTM.
from keras.models import Model
from keras.layers import Input, Dense, LSTM, Dropout
def get_model():
input = Input(shape=(1, 58))
x = LSTM(200, dropout=.0)(input)
x = Dropout(.5)(x)
activation = Dense(1, activation='linear')(x)
model = Model(inputs=input, outputs=activation)
optimizer = keras.optimizers.Adam(lr=0.01,
beta_1=0.9,
beta_2=0.999,
epsilon=None,
decay=0.001,
amsgrad=False)
model.compile(loss='mean_absolute_error', optimizer=optimizer)
model.summary()
return model
get_model()
Resultados e conclusão
A nossa rede está definida, agora podemos treina-la e avaliar os resultados no conjunto de validação. Assim como na definição dos parâmetros da rede. Usando a arquitetura acima, com 50 épocas e batch de 128, chegamos ao ponto de estabilidade das perdas no conjunto de treino e desenvolvimento.
def train_model(model, X_train, Y_train, validation, callbacks):
model.fit(X_train, Y_train, epochs=50, batch_size=128, validation_data=validation, callbacks=callbacks)
return model
model = train_model(get_model(), X_train, Y_train, (X_dev, Y_dev), [plot_losses])
Durante o processo de treinamento e validação, o erro da validação ficou na faixa de 40/50 aluguéis, enquanto o erro do treinamento ficou na faixa dos 20 aluguéis. Para efeitos de comparação, a média de aluguéis a cada hora está em 189. Abaixo, o gráfico de perda desse processo de treinamento.
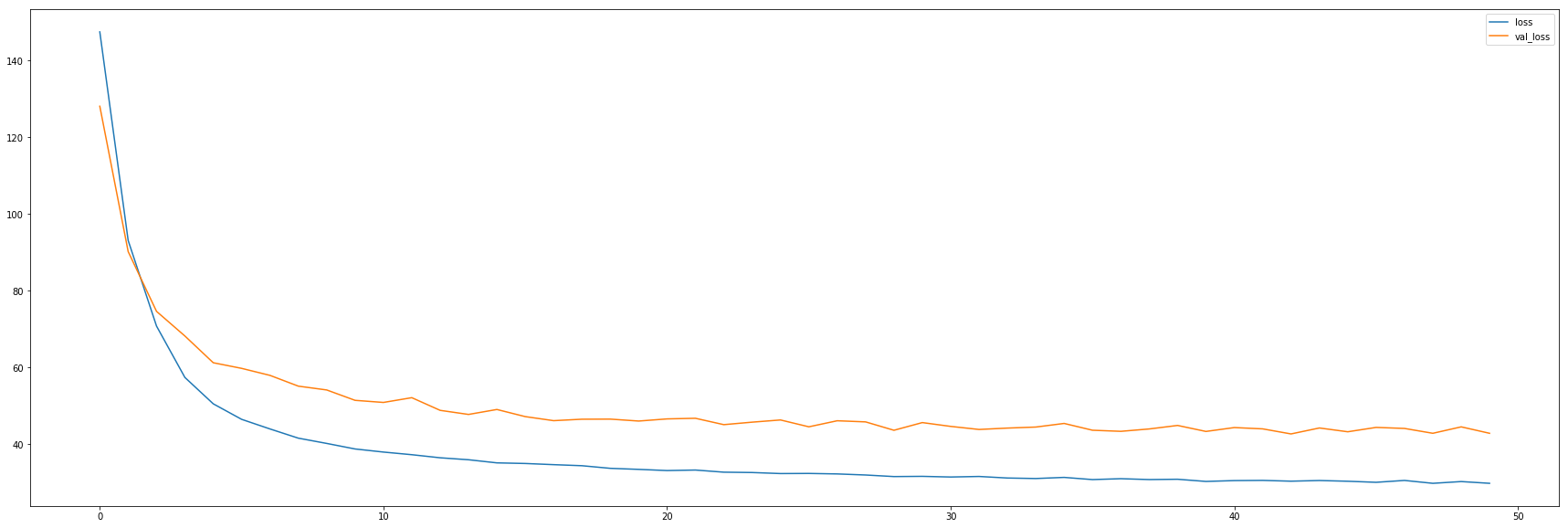
Para problemas de séries temporais é interessante observar os dados sequencialmente para entender em que situações a rede está errando. Segue abaixo o código para plotar o resultado observado e o predito pela rede, possibilitando assim a visualização dos resultados.
from sklearn.metrics import mean_absolute_error
def show_predict(model, X, Y):
Y_predict = model.predict(X)
plt.figure(figsize=(40,10))
plt.plot(list(range(len(Y))), Y, label="Real")
plt.plot(list(range(len(Y_predict))), Y_predict, label="Predicted")
plt.legend()
plt.show()
return mean_absolute_error(Y, Y_predict)
show_predict(model, X_val[:360], Y_val[:360])
show_predict(model, X_val[360:720], Y_val[360:720])
Comparando o real do conjunto de validação com o projetado, obtemos um erro similar similar ao conjunto de dev.

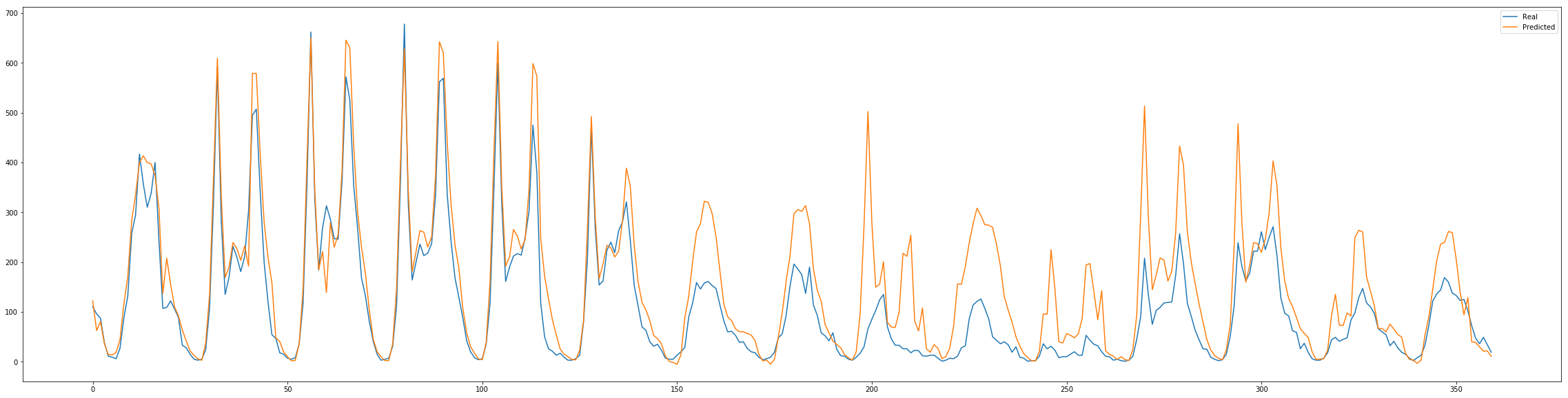
A partir desse resultado inicial, seria interessante fazer uma análise mais extensa, para um ajuste fino da rede e entender melhor as particularidades do dataset, mas esses resultados já mostram que as redes recorrentes têm uma ótima capacidade de se adaptar a esses problemas de séries temporais. Combinando essa poder das redes recorrentes com a facilidade de implementação, usar uma LSTM é um ótimo ponto de partida para esses problemas de séries temporais.
Notas
-
Nessa seção, foi feito um resumo das análises, os gráficos e os códigos dessa análise estão nesse notebook. ↩
-
O Dropout é uma técnica de regularização que pode ser aplicada em qualquer rede, apesar de termos uma analogia em termos de funcionamento, o objetivo dos gates e da técnica de dropout são diferentes. ↩