Deep Learning + Sentiment Analysis
Semanas atrás, tive a oportunidade de fazer um excelente curso da Unicamp de redes neurais na área de processamento de imagens. Sendo um ignorante em deep learning e processamento de imagens, achei uma boa ideia aplicar os conceitos de deep learning em uma área que eu tenho mais familariedade.
Eu já tinha visto o artigo “Natural Language Processing (almost) from Scratch”, que propôs a adaptação dos conceitos de deep learning para a área de PLN, mas na época seria necessário muito trabalho para implementar uma solução. Agora, com as bibliotecas de deep learning e word embeddings disponíveis, a tarefa ficou mais simples.
Nesse post, vou explicar como implementei uma rede convolucional para análise de sentimentos, usando o Keras como framework de deep learning e os word embeddings do Fasttext do Facebook.
DISCLAIMER: não obtive bons resultados com essa solução, para o meu problema obtive desempenho similar a classificadores mais simples.
A grande diferença: convoluções
Para iniciar, é interessante entender dois conceitos que diferenciam o deep learning dos modelos de bag of words usado em classificadores “padrão”.
O bag of words não é tão popular por acaso, a sua simplicidade é uma vantagem chave. Para o domínio de PLN, manter as coisas simples é especialmente importante, já que um dilema comum é a generalização das soluções entre idiomais diferentes. À medida em que as técnicas começam a exigir ferramentas sofisticadas (e.g. ontologias, taggeadores e parsers), mais complicado é utilizar essas soluções em diferentes idiomas. Podemos considerar que a “navalha de Occamm” é mais afiada nesse domínio que nos demais.
O deep learning lida com esse dilema oferecendo uma solução mais sofisticada que o tradicional bag of words, mas sem exigir muitas ferramentas e outros recursos adicionais para funcionar. Isso torna a tecnologia promissora para nós, falante de idiomas menos populares, principalmente pelo poder de generalização que as redes neurais tem mostrado em outros domínios.
A ideia principal por trás dessas redes neurais é o uso de convoluções com word embeddings, técnica que permite obter informação mais rica dos textos e reaproveitar treinamento de outros modelos.
Word embeddings
O conceito de word embeddings não é novo, existe há 20 anos pelo menos, mas se tornou um recurso mais interessante agora que temos disponíveis massas de dados públicas gigantescas para trabalhar.
A ideia é representar cada palvra como um vetor de \(k\) dimensões, de uma forma que a distribuição desses vetores no espaço reflita conceitos do mundo real. Por exemplo, um estudo recente avaliou algumas propriedades desses vetores e, uma das descobertas mais interessantes, foi uma relação de gênero contida nos vetores. Aplicando operações aritméticas entre os word embeddings, foi possível flexionar o gênero de uma palavra
\[king - man + woman = queen\]O ideal é que várias dessas propriedades estejam latentes nos vetores, traduzindo informações semânticas das palavras para esse espaço \(k\)-dimensional. Em um representação do tipo bag of words, as palavras não possuem significado semântico, sendo diferenciadas apenas pela distribuição das mesmas no corpus.
O algoritmo utilizado para gerar esses vetores é o Skip-gram, na documentação do tensorflow, há uma explicação didática de como esses vetores são estimados. De forma superficial, a ideia é otimizar uma função para prever o contexto das palavras, ou seja: dado que uma palavra \(w\) aparaceu, que outras palavras são prováveis de aparecer ao seu entorno?
Facilitando nossa vida, o Facebook liberou word-embeddings criados a partir da Wikipedia para diversos idiomas, incluindo o português. Além de lidar com palavras completas, o algoritmo aprimorado também lida com n-gramas (sub-palavras), trabalhando melhor com linguagens ditas morfologicamente ricas, como turco e finlandês por exemplo, que possuem muitas palavras raras baseadas na composição de outras palavras menores.
O uso desses vetores gerados pelo Facebook não poderia ser mais simples, existe um wrapper em Python para utiliza-los como um mapa do Python, cada palavra é retornada como uma lista de floats. O único porém é que esse wrapper carrega todas as palavras em memória, tornando a aplicação bem agressiva em termos de consumo de memória.
import fasttext
dictionary = fasttext.load_model('resources/wiki.pt/wiki.pt.bin')
exemplo_embeddeding = dictionary['exemplo'])
type(exemplo_embeddeding) # <class 'list'>
len(exemplo_embeddeding) # 300
Utilizando esses vetores, conseguimos alguma informação a priori dos conceitos que estão relacionados com as palavras antes mesmo do treinamento. De certa forma, é uma espécide transfer learning que está sendo feito com essa estratégia de word embeddings pré-treinados.
E agora, como usar esses vetores em uma rede neural?
Convoluções
No domínio de PLN, a convolução funciona como uma combinação linear aplicada a um trecho do texto. Em uma rede neural, diversas convoluções são aplicadas sobre o texto na forma de uma “janela deslizante” para extrair informações de cada parte do texto. É um pouco confuso explicando dessa forma, mas com um exemplo é mais fácil entender o conceito
Considere que estamos usando word embeddings de apenas 2 dimensões, temos como entrada a string “A candidata foi apresentada como alguém que sabe dialogar” e estamos calculando a convolução \(c = [1,0,0,2,1,1]\). No diagrama abaixo, é mostrado o conceito de janela deslizante aplicado sobre a entrada.
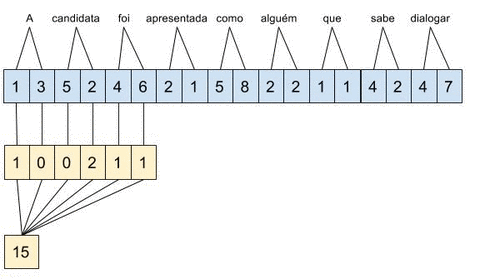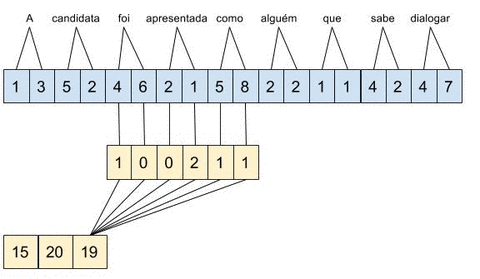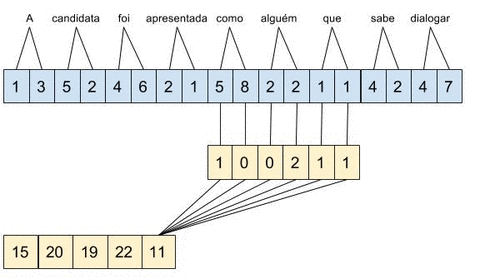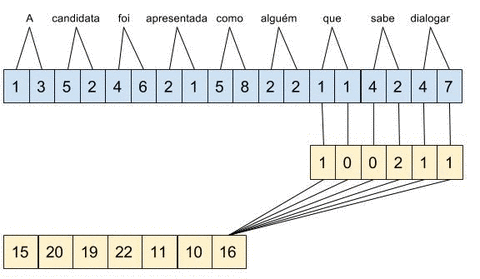
A convolução \(c\) tem tamanho 3 e stride de 1, ou seja, a combinação é aplicada sobre três word embeddings e a janela é deslocada palavra a palavra.
Os valores da convolução são determinados pelo backpropagation, da mesma forma que ocorre com outros pesos. Uma rede neural possue várias convoluções, possivelmente de tamanhos variados.
Intuitivamente, a ideia é que cada convolução extraia um tipo diferente de informação do texto para a classificação. É a mesma ideia de filtros utilizados no domínio de imagens, mas são definidos durante o treinamento, e não a priori com objetivos específicos definidos pelo usuário.
Uma questão do uso de convoluções é que a camada de entrada passa a ter tamanho variável: quanto maior a entrada, maior a saída. A solução é usar o maior tamanho de entrada possível e usar embeddings de padding para complementar o vetor de entrada para as entradas menores.
Esse vetor de padding pode ser um vetor com valor aleatório ou um vetor zerado, para esse problema em específico utilizei um vetor zerado. Optei por um vetor zerado pois os paddings não parece ser uma informação relevante nesse contexto, é diferente de um POS-tagger no qual é muito importante saber se a palavra tem vizinhos ou não para definir a classe gramatical.
Compreendido como as convoluções funcionam, agora devemos entender como essa informação é propagada para a rede até a camada de saída. Essa parte não é muito diferente de uma rede neural tradicional, contendo camadas densas intermediárias e uma camada de ativação ao final.
Arquitetura da rede
Depois da camada de entrada, chegamos em um dos pontos de maiores dificuldades das redes neurais: a necessidade de definir vários hiper-parâmetros e a arquitetura das camadas intermediárias. Infelizmente, esse problema só se agravou com o deep learning, que utiliza redes com diversas camdas intermediárias com os mais diversos objetivos.
Nesse caso, vou aproveitar uma arquitetura proposta no artigo “Convolutional Neural Networks for Sentence Classification”. Provavelmente já existem outras arquiteturas para o problema de análise de sentimentos, simplesmente escolhi a que parece ser uma das primeiras propostas para esse problema.
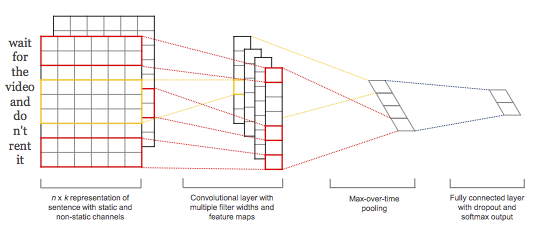
Apesar de eu estar repetindo o termo deep learning durante todo o post, essa rede tem apenas 3 camadas intermediárias. A camada convulocional contém 300 convoluções, sendo 100 de tamanho 3, 100 de tamanho 4 e 100 de tamanho 5. A saída dessas 300 convoluções está conectada a uma camada de Max-Pooling, o que significa que apenas o deslocamento de maior valor será passado propagado para a próxima camada. No exemplo de convolução apresentado acima, o valor 22, obtido ao aplicar a convolução no trecho “apresentada como alguém”, seria propagada para as próximas camadas enquanto os demais trechos seriam desconsiderados para essa convolução.
Ao final da camada Max-Pooling, está conectada de forma densa a camada de saída softmax com três neurônios: positiva, neutra ou negativa.
Para regularização, a rede usa dois mecanismos, uma camada de Dropout após o Max-Pooling e uma restrição \(L2 \leq 3\) para o peso das camadas. A camada de Dropout desativa alguns neurônios aleatoriamente durante o treino para generalizar melhor rede. A restrição \(L2\) é aplicada se \(\| \mathbf{w}\| > 3\), sendo \(\| \mathbf{w}\|\) a norma do vetor de pesos da camada. A regularização é aplicada re-escalando o vetor para \(\|\mathbf{w}\| = 3\), evitando assim que a separação do espaço fiquei muito “tortuosa”.
Abaixo, o código usado para criação dessa rede neural, o único parâmetro necessário é o tamanho máximo da entrada.
def get_model(max_len_pargraph: int) -> Model:
input_sequence = Input(shape=(max_len_pargraph, 300), dtype='float32')
x = Conv1D(filters=100,
kernel_size=3,
activation='relu',
name='convolution_3',
input_shape=(max_len_pargraph, 300))(input_sequence)
convolution3 = MaxPooling1D(max_len_pargraph - 3 + 1)(x)
x = Conv1D(filters=100,
kernel_size=4,
activation='relu',
name='convolution_4',
input_shape=(max_len_pargraph, 300))(input_sequence)
convolution4 = MaxPooling1D(max_len_pargraph - 4 + 1)(x)
x = Conv1D(filters=100,
kernel_size=5,
activation='relu',
name='convolution_5',
input_shape=(max_len_pargraph, 300))(input_sequence)
convolution5 = MaxPooling1D(max_len_pargraph - 5 + 1)(x)
x = keras.layers.concatenate([convolution3, convolution4, convolution5])
x = Dropout(.5)(x)
x = Dense(3, name='dense_layer')(x)
x = Flatten()(x)
results = Activation('softmax')(x)
model = Model(input_sequence, results)
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss="categorical_crossentropy",
optimizer=opt,
metrics=["accuracy"])
model.summary()
return model
Ao final, junto das camadas é definido o algoritmo de otimização. Como é comum nesses algorimos, foi utilizado o gradiente descendente estocástico. Após compilar o modelo, é interessante olhar o summary para verificar se a rede foi construída do jeito esperado.
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_1 (InputLayer) (None, 229, 300) 0
____________________________________________________________________________________________________
convolution_3 (Conv1D) (None, 227, 100) 90100
____________________________________________________________________________________________________
convolution_4 (Conv1D) (None, 226, 100) 120100
____________________________________________________________________________________________________
convolution_5 (Conv1D) (None, 225, 100) 150100
____________________________________________________________________________________________________
max_pooling1d_1 (MaxPooling1D) (None, 1, 100) 0
____________________________________________________________________________________________________
max_pooling1d_2 (MaxPooling1D) (None, 1, 100) 0
____________________________________________________________________________________________________
max_pooling1d_3 (MaxPooling1D) (None, 1, 100) 0
____________________________________________________________________________________________________
concatenate_1 (Concatenate) (None, 1, 300) 0
____________________________________________________________________________________________________
dropout_1 (Dropout) (None, 1, 300) 0
____________________________________________________________________________________________________
dense_layer (Dense) (None, 1, 3) 903
____________________________________________________________________________________________________
flatten_1 (Flatten) (None, 3) 0
____________________________________________________________________________________________________
activation_1 (Activation) (None, 3) 0
====================================================================================================
Total params: 361,203.0
Trainable params: 361,203.0
Non-trainable params: 0.0
____________________________________________________________________________________________________
Callback para regularização dos pesos
A regularização de pesos proposta pelo artigo não está implementada nativamente pelo Keras, para contornar essa limitação é possível usar o recurso de callbacks. Herdando uma classe com vários métodos chamados durante o treinamento, é possível sobrescrever esses métodos para realizar a tarefa desejada.
Na proposta original da rede, a regularização é feita a cada descida no gradiente, o mais próximo que o callback do Keras oferece é ao final de cada batch. O método on_batch_end foi sobrescrito para aplicar a regularização L2 no peso dos vetores:
def on_batch_end(self, batch, logs={}):
for layer_name in ['convolution_3', 'convolution_4', 'convolution_5', 'dense_layer']:
layer = self.model.get_layer(layer_name)
weigths = np.array(layer.get_weights())
original_shape = weigths[0].shape
flatten_weights = weigths[0].flatten()
norm_value = np.linalg.norm(flatten_weights)
if (norm_value > self.max_norm):
norm_flatten_weights = (flatten_weights / norm_value) * self.max_norm
weigths[0] = np.reshape(norm_flatten_weights, original_shape)
layer.set_weights(weigths)
return
No artigo não ficou claro (ou eu não entendi) em qual camada essa regularização foi aplicada, na dúvida apliquei na camada densa e nas convolucionais. Para cada camada, é verifica se o valor da norma passou do limiar, em caso positivo normaliza o vetor. Implementado ao final dos batches, os pesos podem ficar acima do permitido, mas não crescem indefinidamente como ocorreria sem a restrição.
Agora já temos a rede construída, a última parte é adaptar a entrada e as etiquetas ao padrão utilizado pelo Keras.
Preparando o treinamento e validação
A entrada da rede neural é uma matriz tridimensional do numpy: quantidade de amostras X tamanho máximo da entrada X dimensão dos word embeddings. Transformando o parágrafo em uma lista de palavras tokenizadas (sem pontos, caracteres especiais, etc…) e passando o tamanho máximo da entrada, o seguinte método gera uma matriz de entrada para a rede neural.
embedded_words = fasttext.load_model('resources/wiki.pt/wiki.pt.bin')
padding_array = np.zeros(300).tolist()
def format_matrix(paragraphs: list, paragraph_length: int) -> np.ndarray:
padded_paragraphs = []
for (i, paragraph) in enumerate(paragraphs):
len_paragraph = len(paragraph)
padded_paragraph = []
for j in range(0, paragraph_length):
if j < len_paragraph:
padded_paragraph.append(embedded_words[paragraph[j]])
else:
padded_paragraph.append(padding_array)
padded_paragraphs.append(padded_paragraph)
return np.array(padded_paragraphs)
As etiquetas devem ser representadas no formato one-hot, para ser usado em conjunto com a camada de saída softmax. Abaixo, como eu converti as etiquetas do meu corpus para esse formato.
def get_label(label: str) -> list:
from_to = {'NG': [1, 0, 0], 'NE': [0, 1, 0], 'PO': [0, 0, 1]}
return from_to[label]
O resultado final deve ser uma matriz bidimensional do numpy: quantidade de amostras X quantidade de categorias.
Uma questão importante é que os embeddings estão sendo tratados como entradas “fixas”, não é possível realizar o backpropagation sobre os word-embeddings. Para tal, é necessário adaptar a entrada ao recurso de word-embeddings do próprio Keras.
Experimentos e resultados
Para avaliar a rede, eu usei um corpus de notícias sobre política em português que construi para meu projeto de mestrado. O corpus é pequeno e a classificação foi feita a nível de parágrafos, são 1042 parágrafos rotulados em três categorias diferentes (negativo, neutro e positivo). Na dissertação, eu testei os algoritmo mais comuns em classificação de textos (Naive Bayes e SVM linear) e um algoritmo mais sofisticado baseado em entropia.
Nos testes, os algoritmos mais simples obtiveram uma acurácia perto de 60 %, enquanto o algoritmo de entropia ficou bem atrás, mais próximo dos 50%. Os detalhes da implementação, os resultados obtidos e os testes estatísticos desses resultados estão explicados com detalhes na dissertação.
A metodologia usada para avaliar a rede neural foi a validação cruzada. Em geral, para deep learning é mais comum separar conjunto de treinamento, validação e teste já que as redes costumam ser complexas e trabalhar melhor com grandes quantidades de dados. Sendo um corpus reduzido e uma rede neural simples, foi viável realizar validação cruzada para validação com 50 épocas e batches de 50 amostras:
compiled_model.fit(X_training, Y_training, epochs=50, batch_size=50, callbacks=[callback])
As minhas esperanças para um melhor resultado com a rede neural eram as vantagens de usar word embeddings com informações a priori e a possibilidade das convoluções extraírem informação relevante que é descartada em um modelo bag of words. Entretanto, não foi isso que aconteceu.
Para resumir, os resultados da rede neural ficaram na faixa de ~ 60% de acurácia como os classificadores mais simples. Assim como eu observei nos demais classificadores, aparentemente o treino não generaliza: a partir de 90% de acurácia no treino, os ganhos com a classificação do conjunto de validação se estabilizam.
Para ir verificando os impactos de mudanças na rede neural (learning rate, regularização, etc…), decidi criar um callback para avaliar o modelo com o conjunto de validação ao final de cada época. No callback, os resultados obtidos no treinamento e na validação de cada época são salvos em uma lista para posterior validação.
def on_epoch_end(self, epoch, logs={}):
validate_logs = self.model.evaluate(self.X_validation, self.Y_validation, verbose=1, sample_weight=None)
full_log = {'train_acc': logs['acc'],
'train_loss': logs['loss'],
'valid_acc': validate_logs[1],
'valid_loss': validate_logs[0]}
self.results.append(full_log)
Avaliando os resultados dessas 500 épocas, é possível observar que a acurácia do treino perde relevância no desempenho real do categorizador à medida que se aproxima de 1 no treino. A correlação entre as acurácias de treino e testes é de somente 0,578.
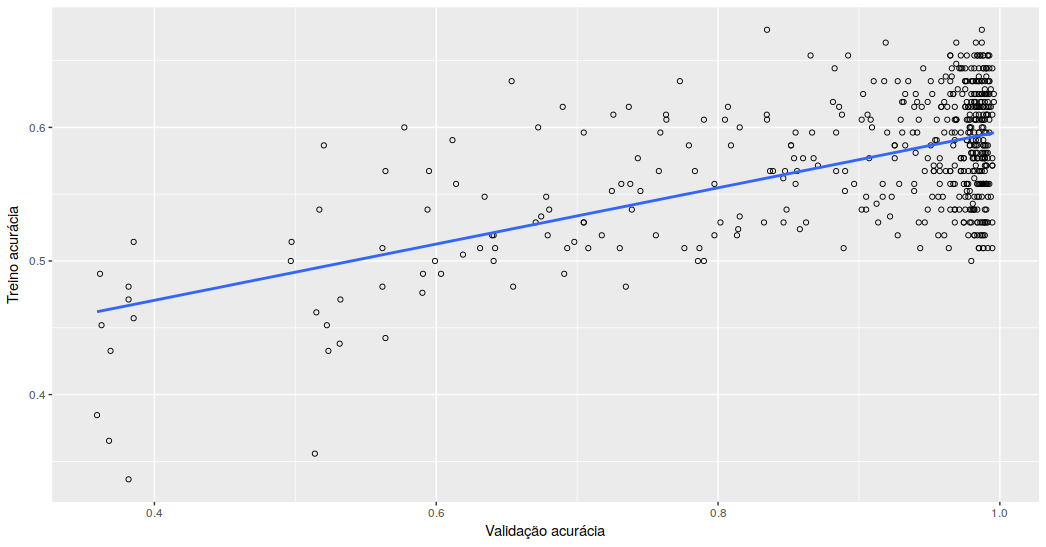
Avaliando apenas as épocas em que a acurácia do treino foi superior a 0,9, totalizando 376 épocas, a correlação cai para 0,055. Ou seja, a partir de 0,9 de acurácia durante o treino, o modelo não obtém mais ganhos expressivos na validação.
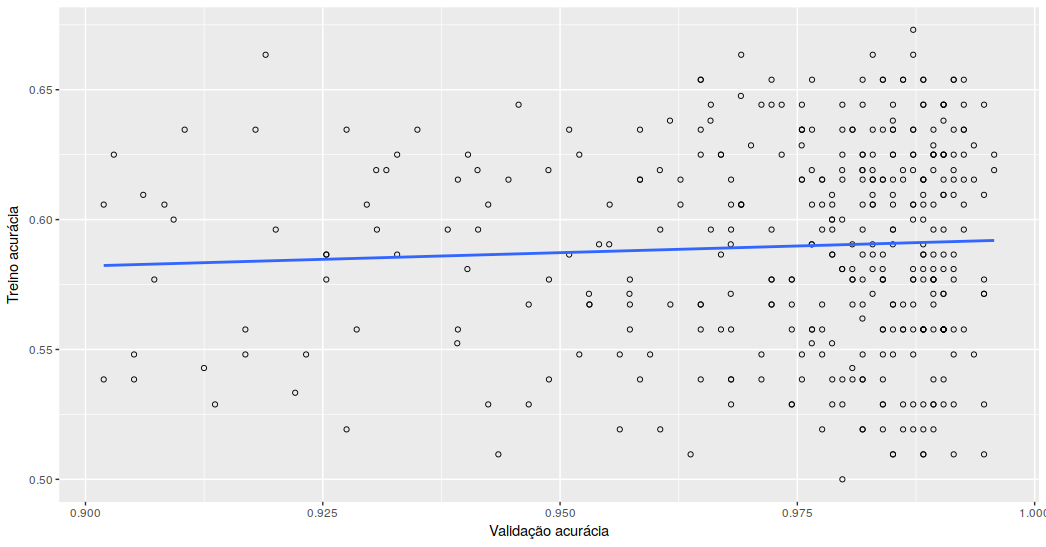
Considerando que outros classificadores também apresentaram resultados similares, não tenho muito expectativas que “tunando” esse modelo eu consiga ganhos relevantes, fiz alguns testes com regularizações mais agressivas e apenas mantiveram ou pioraram os resultados.
Acredito que esse conjunto seja muito pequeno para se generalizar, afinal a precisão no treino chega a quase 1. Em geral, para treino com redes neurais é necessário um grande volume de dados, o que definitivamente não é o caso desse corpus.
Conclusão
Hoje há várias ferramentas para implementar uma redes neurais, os códigos apresentados aqui são bastante simples ao meu ver. Isso facilita e incentiva o uso dessas redes “no mundo real” e facilita a experimentação, questão importante nas redes neurais considerando a infinidade de configurações possíveis para elas.
Não obtive bons resultados com esse algoritmo, mas estou bem longe das condições ideais de uso e a análise de sentimentos, em domínios complexos como notícias, realmente não apresenta desempenho muito bom por diversos motivos.
A ideia era ganhar familariedade com a tecnologia, desenvolver algo do começo ao fim. Os próximos passos seriam aprimorar essa rede neural ou procurar algum outro coprus para obter resultados melhores, inclusive aceito sugestões de experimentos. :)
O código dessa aplicação está disponível no GitHub.